
【题目】数学复习课上,张老师出示了下框中的问题:
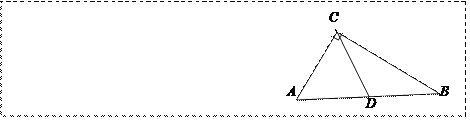
已知:在Rt△ACB中,∠C=90°,点D是斜边AB上的中点,连接CD.
求证:CD=![]() AB.
AB.
问题思考
(1)经过独立思考,同学们想出了多种正确的证明思想,其中有位同学的思路如下:如图1,过点B作BE∥AC交CD的延长线于点E。请你根据这位同学的思路提示证明上述框中的问题.
方法迁移
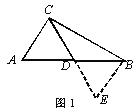
(2)如图2,在Rt△ACB中,∠ACB=90°,点D为AB的中点,点E是线段AC上一动点,连接DE,线段DF始终与DE垂直且交BC于点F。试猜想线段AE,EF,BF之间的数量关系,并加以证明.
拓展延伸
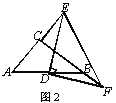
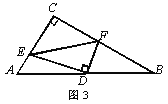
(3)如图3,在Rt△ACB中,∠ACB=90°,点D为AB的中点,点E是线段AC延长线上一动点,连接DE,线段DF始终与DE垂直且交CB延长线于点F。试问第(2)小题中线段AE,EF,BF之间的数量关系会发生改变吗?若会,请写出关系式;若不会,请说明理由.
【答案】(1)CD=![]() AB;(2)AE2+BF2=EF2;(3)线段AE、EF、FB的数量关系不会发生改变,仍有AE2+BF2=EF2.
AB;(2)AE2+BF2=EF2;(3)线段AE、EF、FB的数量关系不会发生改变,仍有AE2+BF2=EF2.
【解析】分析:(1)证ΔACD≌ΔBED和△ACB≌△EBC得证;
(2)如图2,过B作BG∥AC交ED延长线于G,连接GF.通过证ΔADE≌ΔBDG和在Rt△BFG中,得到AE2+BF2=EF2.
(3)如图3,过A作AG//BC交FD的延长线于点G,连接EG,类似(2)问,通过证ΔADG≌ΔBDF,将AE、BF、EF移至Rt△AEG中,可得AE2+BF2=EF2.
详解:(1)证明:∵在⊿ABC中,∠C=90°,D是斜边AB中点,
过B作BE//AC交CD延长线于E,
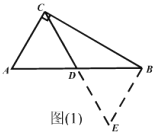
∴∠CAB=∠ABE, ∠ACE=∠BEC,
∴⊿ADC∽⊿BDE,∴D为CE中点,
∵∠CAB+∠CBA=90°,∠ABE+∠CBA=90°,
∴⊿ABC≌⊿ECB,AB=CE,
∴CD=![]() AB.
AB.
(2)证明:过B作BG//AC交ED延长线于G,连接GF.
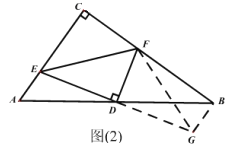
∴∠EAD=∠GBD,又∠EDA=∠GDB,AD=DB,
∴ΔAED≌ΔBDG,∴AE=BG,DE=DG,
又∵DF⊥DE,∴DF是EG中垂线,EF=GF,
∵∠C=90,∠GBF=90,∴BF2+BG2=GF2;
∴AE2+BF2=EF2.
(3)线段AE、EF、FB的数量关系不会发生改变,仍有AE2+BF2=EF2.
证明:如图3,过A作AG//BC交FD的延长线于点G,连接EG,
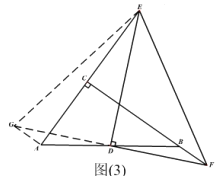
∵AG//BC,∴∠GAD=∠DBF,∠AGD=∠DFB,
∵点D为AB的中点,∴AD=DB,
∴⊿ADG≌⊿BDF,∴AG=BF,GD=DF,
∵DE⊥DF,∴EF=EG,
∵AG//BC,∠EAG=∠ACB=90°,
∴AE2+AG2=EG2,
∴AE2+BF2=EF2.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
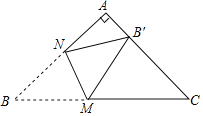
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=![]() +1,点M,N分别是边BC,AB上的动点,沿MN所在的直线折叠∠B,使点B的对应点B′始终落在边AC上,若△MB′C为直角三角形,则BM的长为_______.
+1,点M,N分别是边BC,AB上的动点,沿MN所在的直线折叠∠B,使点B的对应点B′始终落在边AC上,若△MB′C为直角三角形,则BM的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
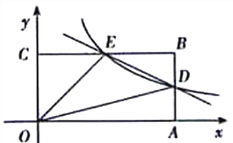
【题目】如图,在平面直角坐标系中,原点O是矩形OABC的一个顶点,点A、C都
在坐标轴上,点B的坐标是(4.2),反比例函数![]() 与AB,BC分别交于点D,E。
与AB,BC分别交于点D,E。
(1)求直线DE的解析式;
(2)若点F为y轴上一点,△OEF和△ODE的面积相等,求点F的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为打造引江枢纽风光带,一段长为1.2千米的河道整治任务交由甲、乙两个工程队接力完成,共用时60天. 已知甲队每天整治24米,乙队每天整治16米.
(1)根据题意,小明、小丽分别列出如下的一元一次方程(尚不完整): 小明:![]() . 小丽:
. 小丽:![]() =60. 请分别指出上述方程中
=60. 请分别指出上述方程中![]() 的意义,并补全方程: 小明:
的意义,并补全方程: 小明:![]() 表示 . 小丽:
表示 . 小丽:![]() 表示 .
表示 .
(2)请选择其中一种方法,求甲、乙两队分别整治河道多少米?(写出完整的解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同.
(1)搅匀后,从中任意摸出一个球,恰好是红球的概率是 ;
(2)搅匀后,从中任意摸出一个球,记录颜色后放回、搅匀,再从中任意摸出一个球.
①求两次都摸到红球的概率;
②经过了n次“摸球﹣记录﹣放回”的过程,全部摸到红球的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:我们知道a的几何意义是在数轴上数a对应的点与原点的距离.数轴上数a与数0对应点之间的距离,![]() 这 个结论可以推广为: |a- b|均表示在数轴上数a与b对应点之间的距离,例:已知|a-1|=2, 求a的值.
这 个结论可以推广为: |a- b|均表示在数轴上数a与b对应点之间的距离,例:已知|a-1|=2, 求a的值.
解:在数轴上与1的距离为2点的对应数为3和-1,即a的值为3和-1.
仿照阅读材料的解法,解决下列问题
(1)已知![]() ,求a的值.
,求a的值.
(2)若数轴上表示a的点在-4与2之间,则|a+4|+|a-2|的值为___
(3)当a满足什么条件时,|a-1|+ |a+2|有最小值,最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义符号min{a,b}的含义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a.如:min{2,﹣4}=﹣4,min{1,5}=1,则min{﹣x2+1,﹣x}的最大值是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】考试前夕,为“连粽连中”的吉祥寓意,某校食堂购进甲、乙两种粽子520个,其中甲种粽子花费600元,乙种粽子花费800元,已知甲种粽子单价比乙种粽子单价高20%,乙种粽子的单价是多少元?甲、乙两种粽子各购买了多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
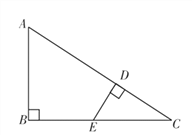
【题目】如图,一艘军舰位于点A处,在其正南方向有一目标B,在点B的正东方向有一目标C,且AB+BC=3海里,在AC上有一艘补给船D,DC为1海里;军舰从点A出发,向AB,BC方向匀速航行,补给船同时从点D出发,沿垂直于AC方向匀速直线航行,欲将一批物品送达军舰.已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了几海里?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com