
【题目】如图,在菱形ABCD中,点E是BC边的中点,动点M在CD边上运动,以EM为折痕将△CEM折叠得到△PEM,联接PA,若AB=4,∠BAD=60°,则PA的最小值是( )

A. ![]() B. 2 C. 2
B. 2 C. 2![]() ﹣2 D. 4
﹣2 D. 4
 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
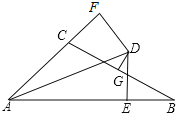
【题目】已知∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,
(1)连接CD、BD,求证:△CDF≌△BDE;
(2)若AE=5,AC=3,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
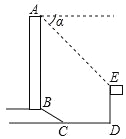
【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆低端D到大楼前梯砍底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:![]() ,则大楼AB的高度为_________米.
,则大楼AB的高度为_________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )

A. 若AD⊥BC,则四边形AEDF是矩形 B. 若BD=CD,则四边形AEDF是菱形
C. 若AD垂直平分BC,则四边形AEDF是矩形 D. 若AD平分∠BAC,则四边形AEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
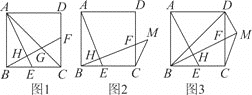
【题目】已知正方形ABCD中,点E,F分别为BC,CD上的点,连接AE,BF相交于点H,且AE⊥BF.
(1)如图1,连接AC交BF于点G,求证:∠AGF=∠AEB+45°;
(2)如图2,延长BF到点M,连接MC,若∠BMC=45°,求证:AH+BH=BM;
(3)如图3,在(2)的条件下,若点H为BM的三等分点,连接BD,DM,若HE=1,求△BDM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=50°,P为△ABC内一点,过点P的直线MN分別交AB、BC于点M、N.若M在PA的中垂线上,N在PC的中垂线上,则∠APC的度数为____________°

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把甲、乙两张形状、大小相同但画面不同的风景图片按同样的方式剪成相同的2段,混合洗匀.
(1)从这堆图片中随机抽出一张,放回混合洗匀,再抽出一张,则抽出的这两张图片恰好 可以拼成同一张风景图片的概率为 ;
(2)从这堆图片中随机抽出两张,求抽出的这两张图片恰好可以组成甲图片的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,在△ABC中,∠C=90°,BC=5cm,AC=7cm. 两个动点P、Q分别从B、C两点同时出发,其中点P以1厘米/秒的速度沿着线段BC向点C运动,点Q以2厘米/秒的速度沿着线段CA向点A运动.
(1)P、Q两点在运动过程中,经过几秒后,△PCQ的面积等于4厘米2?经过几秒后PQ的长度等于5厘米?
(2)在P、Q两点在运动过程中,四边形ABPQ的面积能否等于11厘米2?试说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com