
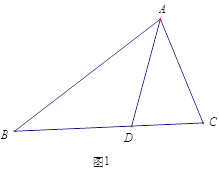
ЁОЬтФПЁПвбжЊЃКШчЭМЫљЪОЃЌдкЁїABCжаЃЌЁЯC=90ЁуЃЌBC=5cmЃЌAC=7cm. СНИіЖЏЕуPЁЂQЗжБ№ДгBЁЂCСНЕуЭЌЪБГіЗЂЃЌЦфжаЕуPвд1РхУз/УыЕФЫйЖШбизХЯпЖЮBCЯђЕуCдЫЖЏЃЌЕуQвд2РхУз/УыЕФЫйЖШбизХЯпЖЮCAЯђЕуAдЫЖЏ.
ЃЈ1ЃЉPЁЂQСНЕудкдЫЖЏЙ§ГЬжаЃЌОЙ§МИУыКѓЃЌЁїPCQЕФУцЛ§ЕШгк4РхУз2ЃПОЙ§МИУыКѓPQЕФГЄЖШЕШгк5РхУзЃП
ЃЈ2ЃЉдкPЁЂQСНЕудкдЫЖЏЙ§ГЬжаЃЌЫФБпаЮABPQЕФУцЛ§ФмЗёЕШгк11РхУз2ЃПЪдЫЕУїРэгЩ.

ЁОД№АИЁПЃЈ1ЃЉОЙ§1УыКѓЃЌЁїPCQЕФУцЛ§ЕШгк4РхУз2ЃЛОЙ§2УыКѓPQЕФГЄЖШЕШгк5РхУзЃЛЃЈ2ЃЉЫФБпаЮABPQЕФУцЛ§ВЛПЩФмЕШгк11РхУз2.
ЁОНтЮіЁП
ЃЈ1ЃЉШєЪЙЦфУцЛ§ЮЊ4ЃЌМДSЁїPCQ= PCQC=4ЃЌДњШыЪ§ОнЧѓНтМДПЩЃЛИљОнЙДЙЩЖЈРэПЩЕУЗНГЬ,МДПЩЧѓГіtЕФжЕ;
PCQC=4ЃЌДњШыЪ§ОнЧѓНтМДПЩЃЛИљОнЙДЙЩЖЈРэПЩЕУЗНГЬ,МДПЩЧѓГіtЕФжЕ;
ЃЈ2ЃЉШєЫФБпаЮABPQЕФУцЛ§ФмЗёЕШгк11ЃЌМДSЁїPCQ= -11=
-11= ЃЌНЈСЂЗНГЬЃЌНтЗНГЬПДЪЧЗёгаНтЃЌШєгаЃЌдђДцдк.
ЃЌНЈСЂЗНГЬЃЌНтЗНГЬПДЪЧЗёгаНтЃЌШєгаЃЌдђДцдк.
ЃЈ1ЃЉЃЈiЃЉЩшОЙ§xУыКѓЃЌЁїPCQЕФУцЛ§ЕШгк4РхУз2ЃЌДЫЪБЃЌPC=5-xЃЌCQ=2x.
гЩЬтвтЃЌЕУ  ЃЌећРэЃЌЕУx2-5x+4=0. НтЕУx1=1ЃЌx2=4.
ЃЌећРэЃЌЕУx2-5x+4=0. НтЕУx1=1ЃЌx2=4.
ЕБx=4ЪБЃЌ2x=8ЃО7ЃЌДЫЪБЕуQдНЙ§AЕуЃЌВЛКЯЬтвтЃЌЩсШЅ.
МДОЙ§1УыКѓЃЌЁїPCQЕФУцЛ§ЕШгк4РхУз2.
ЃЈiiЃЉЩшОЙ§tУыКѓPQЕФГЄЖШЕШгк5РхУз. гЩЙДЙЩЖЈРэЃЌЕУ(5-t)2+(2t)2=52 .
ећРэЃЌЕУt2-2t=0. НтЕУt1=2ЃЌt2=0(ВЛКЯЬтвтЃЌЩсШЅ).
Д№ЃКОЙ§2УыКѓPQЕФГЄЖШЕШгк5РхУз.
ЃЈ2ЃЉЩшОЙ§mУыКѓЃЌЫФБпаЮABPQЕФУцЛ§ЕШгк11РхУз2.гЩЬтвтЃЌЕУ .ећРэЃЌЕУm2-5m+6.5=0.
.ећРэЃЌЕУm2-5m+6.5=0.
ЁпЁї=(-5)2-4ЁС6.5=-1ЃМ0ЃЌ ЁрЗНГЬУЛгаЪЕЪ§Иљ.
МДЫФБпаЮABPQЕФУцЛ§ВЛПЩФмЕШгк11РхУз2.


 бєЙтПЮЬУПЮЪБзївЕЯЕСаД№АИ
бєЙтПЮЬУПЮЪБзївЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкСтаЮABCDжаЃЌЕуEЪЧBCБпЕФжаЕуЃЌЖЏЕуMдкCDБпЩЯдЫЖЏЃЌвдEMЮЊелКлНЋЁїCEMелЕўЕУЕНЁїPEMЃЌСЊНгPAЃЌШєAB=4ЃЌЁЯBAD=60ЁуЃЌдђPAЕФзюаЁжЕЪЧЃЈЁЁЁЁЃЉ

A. ![]() B. 2 C. 2
B. 2 C. 2![]() Љ2 D. 4
Љ2 D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌЁїABCжаЃЌADЪЧЁЯBACЕФНЧЦНЗжЯпЃЌШєAB=AC+CD.ФЧУДЁЯACB гыЁЯABCгадѕбљЕФЪ§СПЙиЯЕ? аЁУїЭЈЙ§ЙлВьЗжЮіЃЌаЮГЩСЫШчЯТНтЬтЫМТЗ:
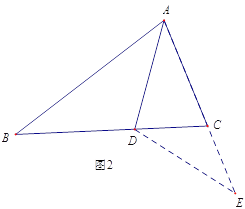
ШчЭМ2,бгГЄACЕНE,ЪЙCE=CD,СЌНгDE,гЩAB=AC+CD,ПЩЕУAE=AB,гжвђЮЊADЪЧЁЯBACЕФЦНЗжЯпЃЌПЩЕУЁїABDЁеЁїAED,НјвЛВНЗжЮіОЭПЩвдЕУЕНЁЯACB гыЁЯABCЕФЪ§СПЙиЯЕ.
(1) ХаЖЈЁїABD гыЁїAED ШЋЕШЕФвРОнЪЧ______________(SSS,SAS,ASA,AAS ДгЦфжабЁдёвЛИі);
(2)ЁЯACB гыЁЯABCЕФЪ§СПЙиЯЕЮЊ:___________________
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЁїABCЕФШ§БпaЃЌbЃЌcЃЌТњзуa+b2+|cЉ6|+28=4![]() +10bЃЌдђЁїABCЕФЭтНгдВАыОЖ=__________ЃЎ
+10bЃЌдђЁїABCЕФЭтНгдВАыОЖ=__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊСЫЗсИЛбЇЩњЕФаЃдАЩњЛюЃЌзМБИЙКНјвЛХњРКЧђКЭзуЧђЃЎЦфжаРКЧђЕФЕЅМлБШзуЧђЕФЕЅМлЖр40дЊЃЌгУ1500дЊЙКНјЕФРКЧђИіЪ§гы900дЊЙКНјЕФзуЧђИіЪ§ЯрЕШЃЎ
ЃЈ1ЃЉРКЧђКЭзуЧђЕФЕЅМлИїЪЧЖрЩйдЊЃП
ЃЈ2ЃЉИУаЃДђЫугУ1000дЊЙКТђРКЧђКЭзуЧђЃЌЮЪЧЁКУгУЭъ1000дЊЃЌВЂЧвРКЧђЁЂзуЧђЖМТђгаЕФЙКТђЗНАИгаФФМИжжЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯп![]() ЃЌжБЯп
ЃЌжБЯп![]() КЭжБЯп
КЭжБЯп![]() ЁЂ
ЁЂ![]() НЛгкЕуCКЭDЃЌЕуPЪЧжБЯп
НЛгкЕуCКЭDЃЌЕуPЪЧжБЯп![]() ЩЯвЛЖЏЕуЃЎ
ЩЯвЛЖЏЕуЃЎ

ЃЈ1ЃЉШчЭМЃЌЕБЕуPдкЯпЖЮCDЩЯдЫЖЏЪБЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() жЎМфДцдкЪВУДЪ§СПЙиЯЕЃПЧыФуВТЯыНсТлВЂЫЕУїРэгЩЃЎ
жЎМфДцдкЪВУДЪ§СПЙиЯЕЃПЧыФуВТЯыНсТлВЂЫЕУїРэгЩЃЎ
ЃЈ2ЃЉЕБЕуPдкCЁЂDСНЕуЕФЭтВрдЫЖЏЪБЃЈPЕугыЕуCЁЂDВЛжиКЯЃЉЃЌЩЯЪіЃЈ1ЃЉжаЕФНсТлЪЧЗёЛЙГЩСЂЃПШєВЛГЩСЂЃЌЧыжБНгаДГі![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() жЎМфЕФЪ§СПЙиЯЕЃЌВЛБиаДРэгЩЃЎ
жЎМфЕФЪ§СПЙиЯЕЃЌВЛБиаДРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃКЖдГЦжс![]() ЕФХзЮяЯп
ЕФХзЮяЯп![]() гы
гы![]() жсЯрНЛгк
жсЯрНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌЦфжаЕу
СНЕуЃЌЦфжаЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЧвЕу
ЃЌЧвЕу![]() дкХзЮяЯп
дкХзЮяЯп![]() ЩЯЃЎ
ЩЯЃЎ

![]() ЧѓХзЮяЯпЕФНтЮіЪНЃЎ
ЧѓХзЮяЯпЕФНтЮіЪНЃЎ
![]() Еу
Еу![]() ЮЊХзЮяЯпгы
ЮЊХзЮяЯпгы![]() жсЕФНЛЕуЃЎ
жсЕФНЛЕуЃЎ
ЂйЕу![]() дкХзЮяЯпЩЯЃЌЧв
дкХзЮяЯпЩЯЃЌЧв![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕузјБъЃЎ
ЕузјБъЃЎ
ЂкЩшЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯЕФЖЏЕуЃЌзї
ЩЯЕФЖЏЕуЃЌзї![]() жсНЛХзЮяЯпгкЕу
жсНЛХзЮяЯпгкЕу![]() ЃЌЧѓЯпЖЮ
ЃЌЧѓЯпЖЮ![]() ГЄЖШЕФзюДѓжЕЃЎ
ГЄЖШЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌаЁЛЊДгвЛИідВаЮГЁЕиЕФAЕуГіЗЂЃЌбизХгыАыОЖOAМаНЧЮЊІСЕФЗНЯђаазпЃЌзпЕНГЁЕиБпдЕBКѓЃЌдйбизХгыАыОЖOBМаНЧЮЊІСЕФЗНЯђелЯђаазпЃЎАДееетжжЗНЪНЃЌаЁЛЊЕкЮхДЮзпЕНГЁЕиБпдЕЪБДІгкЛЁABЩЯЃЌдђІСШЁжЕЗЖЮЇЪЧЃЈ ЃЉ

A. 36Ёу![]() 45Ёу B. 45Ёу
45Ёу B. 45Ёу![]() 54Ёу C. 54Ёу
54Ёу C. 54Ёу![]() 72Ёу D. 72Ёу
72Ёу D. 72Ёу![]() 90Ёу
90Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЖўДЮКЏЪ§
жаЃЌЖўДЮКЏЪ§![]() ЕФЭМЯѓгы
ЕФЭМЯѓгы![]() жсе§АыжсНЛгк
жсе§АыжсНЛгк![]() ЕуЃЎ
ЕуЃЎ
![]() ЧѓжЄЃКИУЖўДЮКЏЪ§ЕФЭМЯѓгы
ЧѓжЄЃКИУЖўДЮКЏЪ§ЕФЭМЯѓгы![]() жсБигаСНИіНЛЕуЃЛ
жсБигаСНИіНЛЕуЃЛ
![]() ЩшИУЖўДЮКЏЪ§ЕФЭМЯѓгы
ЩшИУЖўДЮКЏЪ§ЕФЭМЯѓгы![]() жсЕФСНИіНЛЕужагвВрЕФНЛЕуЮЊЕу
жсЕФСНИіНЛЕужагвВрЕФНЛЕуЮЊЕу![]() ЃЌШє
ЃЌШє![]() ЃЌНЋжБЯп
ЃЌНЋжБЯп![]() ЯђЯТЦНвЦ
ЯђЯТЦНвЦ![]() ИіЕЅЮЛЕУЕНжБЯп
ИіЕЅЮЛЕУЕНжБЯп![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
![]() дк
дк![]() ЕФЬѕМўЯТЃЌЩш
ЕФЬѕМўЯТЃЌЩш![]() ЮЊЖўДЮКЏЪ§ЭМЯѓЩЯЕФвЛИіЖЏЕуЃЌЕБ
ЮЊЖўДЮКЏЪ§ЭМЯѓЩЯЕФвЛИіЖЏЕуЃЌЕБ![]() ЪБЃЌЕу
ЪБЃЌЕу![]() Йигк
Йигк![]() жсЕФЖдГЦЕуЖМдкжБЯп
жсЕФЖдГЦЕуЖМдкжБЯп![]() ЕФЯТЗНЃЌЧѓ
ЕФЯТЗНЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com