
【题目】如图:对称轴![]() 的抛物线
的抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,其中点
两点,其中点![]() 的坐标为
的坐标为![]() ,且点
,且点![]() 在抛物线
在抛物线![]() 上.
上.

![]() 求抛物线的解析式.
求抛物线的解析式.
![]() 点
点![]() 为抛物线与
为抛物线与![]() 轴的交点.
轴的交点.
①点![]() 在抛物线上,且
在抛物线上,且![]() ,求点
,求点![]() 点坐标.
点坐标.
②设点![]() 是线段
是线段![]() 上的动点,作
上的动点,作![]() 轴交抛物线于点
轴交抛物线于点![]() ,求线段
,求线段![]() 长度的最大值.
长度的最大值.
【答案】(1) ![]() ;(2) 点
;(2) 点![]() 的坐标为
的坐标为![]() 或
或![]() ;(3)当
;(3)当![]() 时,
时,![]() 有最大值
有最大值![]() .
.
【解析】
(1)因为抛物线的对称轴为x=-1,A点坐标为(-3,0)与(2,5)在抛物线上,代入抛物线的解析式,即可解答;
(2)①先由二次函数的解析式为y=x2+2x-3,得到C点坐标,然后设P点坐标为(x,x2+2x-3),根据S△POC=4S△BOC列出关于x的方程,解方程求出x的值,进而得到点P的坐标;
②先运用待定系数法求出直线AC的解析式为y=-x-3,再设Q点坐标为(x,-x-3),则D点坐标为(x,x2+2x-3),然后用含x的代数式表示QD,根据二次函数的性质即可求出线段QD长度的最大值.
![]() 因为抛物线的对称轴为
因为抛物线的对称轴为![]() ,
,![]() 点坐标为
点坐标为![]() 与
与![]() 在抛物线上,则:
在抛物线上,则:
 ,
,
解得: .
.
所以抛物线的解析式为:![]() .
.
![]() 二次函数的解析式为
二次函数的解析式为![]() ,
,
∴抛物线与![]() 轴的交点
轴的交点![]() 的坐标为
的坐标为![]() ,
,![]() .
.
设![]() 点坐标为
点坐标为![]() ,
,

∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .当
.当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
∴点![]() 的坐标为
的坐标为![]() 或
或![]() ;
;
![]() 设直线
设直线![]() 的解析式为
的解析式为![]() ,将
,将![]() ,
,![]() 代入,
代入,
得![]() ,
,
解得:![]() .
.
即直线![]() 的解析式为
的解析式为![]() .
.
设![]() 点坐标为
点坐标为![]() ,则
,则![]() 点坐标为
点坐标为![]() ,
,
![]() ,
,
∴当![]() 时,
时,![]() 有最大值
有最大值![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=50°,P为△ABC内一点,过点P的直线MN分別交AB、BC于点M、N.若M在PA的中垂线上,N在PC的中垂线上,则∠APC的度数为____________°

查看答案和解析>>
科目:初中数学 来源: 题型:
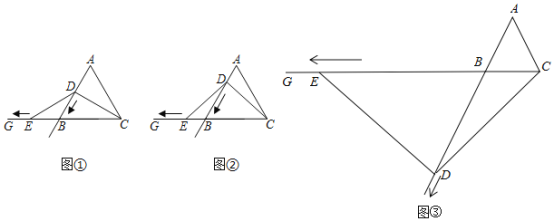
【题目】如图,△ABC是等边三角形,点D、E分别是射线AB、射线CB上的动点,点D从点A出发沿射线AB移动,点E从点B出发沿BG移动,点D、点E同时出发并且运动速度相同.连接CD、DE.
(1)如图①,当点D移动到线段AB的中点时,求证:DE=DC.
(2)如图②,当点D在线段AB上移动但不是中点时,试探索DE与DC之间的数量关系,并说明理由.
(3)如图③,当点D移动到线段AB的延长线上,并且ED⊥DC时,求∠DEC度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,在△ABC中,∠C=90°,BC=5cm,AC=7cm. 两个动点P、Q分别从B、C两点同时出发,其中点P以1厘米/秒的速度沿着线段BC向点C运动,点Q以2厘米/秒的速度沿着线段CA向点A运动.
(1)P、Q两点在运动过程中,经过几秒后,△PCQ的面积等于4厘米2?经过几秒后PQ的长度等于5厘米?
(2)在P、Q两点在运动过程中,四边形ABPQ的面积能否等于11厘米2?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的顶点为
的顶点为![]() ,直线
,直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点.
两点.![]() 是抛物线上一点,过
是抛物线上一点,过![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .如果以
.如果以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,那么点
相似,那么点![]() 的坐标是________.
的坐标是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:


请根据以上图表信息解答下列问题:
(1)频数分布表中的m=________,n=________;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为________°;
(3)从选择“篮球”选项的60名学生中,随机抽取10名学生作为代表进行投篮测试,则其中某位学生被选中的概率是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经销商经销某种农产品,在一个销售月内,每售出1吨该产品获利500元,未售出的产品,每1吨亏损300元.根据历史资料记载的20个月的销售情况,得到如图所示的销售月内市场需求量的频数分布直方图.经销商为下一个销售月购进了130吨该农产品,以x(单位:吨,100≤x≤150)表示下一个销售月内的市场需求量,T(单位:元)表示下一个销售月内经销该农产品的利润.
完成下列问题:

(1)根据直方图可以看出,销售月内市场需求量的中位数在第_________组.
(2)当100≤x≤150时,用含x的代数式或常数表示T;
(3)根据直方图估计利润T不少于57000元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,∠BAD是△ABC的一个外角,∠BAC、∠BAD的平分线分别交⊙O于点E、F.请你在图上连接EF.(1)证明:EF是⊙O的直径;(2)请你判断EF与BC有怎样的位置关系?并请证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果二次函数y=x2+(k+2)x+k+5的图象与x轴的两个不同交点的横坐标都是正的,那么k值应为( )
A. k>4或k<﹣5 B. ﹣5<k<﹣4 C. k≥﹣4或k≤﹣5 D. ﹣5≤k≤﹣4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com