
【题目】如图,一只蚂蚁在正方形ABCD区域内爬行,点O是对角线的交点,∠MON=90°,OM,ON分别交线段AB,BC于M,N两点,则蚂蚁停留在阴影区域的概率为 . 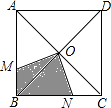
【答案】![]()
【解析】解:∵四边形ABCD为正方形,点O是对角线的交点, ∴∠MBO=∠NCO=45°,OB=OC,∠BOC=90°,
∵∠MON=90°,
∴∠MOB+∠BON=90°,∠BON+∠NOC=90°,
∴∠MOB=∠NOC.
在△MOB和△NOC中,有  ,
,
∴△MOB≌△NOC(ASA).
同理可得:△AOM≌△BON.
∴S阴影=S△BOC= ![]() S正方形ABCD .
S正方形ABCD .
∴蚂蚁停留在阴影区域的概率P= ![]() =
= ![]() .
.
故答案为: ![]() .
.
根据正方形的性质可得出“∠MBO=∠NCO=45°,OB=OC,∠BOC=90”,通过角的计算可得出∠MOB=∠NOC,由此即可证出△MOB≌△NOC,同理可得出△AOM≌△BON,从而可得知S阴影= ![]() S正方形ABCD , 再根据几何概率的计算方法即可得出结论.
S正方形ABCD , 再根据几何概率的计算方法即可得出结论.


科目:初中数学 来源: 题型:
【题目】填空并在括号内加注理由。
如图,已知![]() ∥
∥![]() ,
,![]() 、
、![]() 分别平分
分别平分![]() 和
和![]()

求证:![]()
证明:∵![]() ∥
∥![]()
∴![]() = ( )
= ( )
∵![]() 、
、![]() 平分
平分![]() 、
、![]()
∴![]() =
=![]()
∴![]() =
=![]() ( )
( )
∴![]() =
=![]()
∴ ∥ ( )
∴![]() =∠ ( )
=∠ ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据下面X与Y的对话解答下列各小题:
X:我和Y都是多边形,我们俩的内角和相加的结果为1440°;
Y:X的边数与我的边数之比为1∶3.
(1)求X与Y的外角和相加的度数;
(2)分别求出X与Y的边数;
(3)试求出Y共有多少条对角线?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )

A. BD=CD B. ∠BAD=∠CAD C. ∠B=∠C D. ∠ADB=∠ADC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC和△MNB中,∠ACB=∠MBN=90°,AC=BC=4,MB=NB= ![]() BC,点N在BC边上,连接AN,CM,点E,F,D,G分别为AC,AN,MN,CM的中点,连接EF,FD,DG,EG.
BC,点N在BC边上,连接AN,CM,点E,F,D,G分别为AC,AN,MN,CM的中点,连接EF,FD,DG,EG. 
(1)判断四边形EFDG的形状,并证明;
(2)如图2,将图1中的△MBN绕点B逆时针旋转90°,其他条件不变,猜想此时四边形EFDG的形状,并证明. 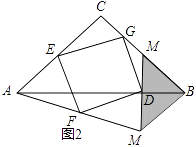
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4,如图2,正方形ABCD顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长. 例如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D,若第二次掷得2,就从D开始顺时针连续跳2个边长,落到圈B,…设游戏者从圈A起跳.
(1)若随机掷一次骰子,求落回到圈A的概率P1;
(2)若随机掷两次骰子,用列表法或树状图法求出最后落回到圈A的概率P.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com