
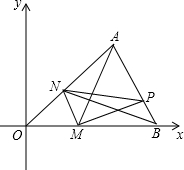
 如图,在平面直角坐标中,△AOB的三个顶点的坐标分别是A(4,4),O(0,0),B(6,0),点M是射线OB上的一动点,过点M作MN∥AB,MN与射线OA交于点N,P是AB边上的任意点,连接AM,PM,PN,BN,设△PMN的面积为S.
如图,在平面直角坐标中,△AOB的三个顶点的坐标分别是A(4,4),O(0,0),B(6,0),点M是射线OB上的一动点,过点M作MN∥AB,MN与射线OA交于点N,P是AB边上的任意点,连接AM,PM,PN,BN,设△PMN的面积为S.分析 (1)由相似三角形的性质即可,
(2)由两直线平行,得到三角形相似,再由相似得到比例式,表示出NH,从而求出S的函数关系式;
(3)利用同高的两个三角形的面积比是底的比,得出MN=2AB,求出OM,得到点M的坐标.
解答 解:(1)如图,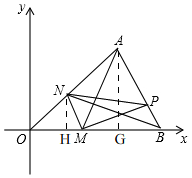
过点N作NH⊥OB,AG⊥OB,
∵MN∥AB,
∴△OMN∽△OAB,
∴$\frac{NH}{AG}=\frac{OM}{OB}$,
∴NH=$\frac{4}{3}$,
∵点N在直线OA上,直线OA的解析式为y=x,
∴N($\frac{4}{3}$,$\frac{4}{3}$);
(2)设OM=x,∵MN∥AB,
∴S△MNB=S△PMN=S,
∵△OMN∽△OBA,
∴$\frac{MN}{AB}=\frac{OM}{OB}$,NH=$\frac{2}{3}$x,
∴S=$\frac{1}{2}$MB×NH=$\frac{1}{2}$(6-x)×$\frac{2}{3}$x=-$\frac{1}{3}$(x-3)2+3,
∴x=3时,S有最大值为3.
(3)假设存在,
设MN与AB之间的距离为h,
若S△PMN=2S△ANB,
∴$\frac{1}{2}$MN×h=2×$\frac{1}{2}$AB×h,
∴MN=2AB,
∵△OMN∽△OBA,
∴$\frac{OM}{OB}$=$\frac{MN}{AB}$=2,
∴OM=12,
∴M(12,0),
若S△ANB=2S△PMN,同理可得M(3,0),
∴M(12,0)或M(3,0).
点评 本题是相似三角形的综合题,主要考查相似三角形的性质和判定,解本题的关键是由相似得出比例式$\frac{OM}{OB}$=$\frac{MN}{AB}$.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 减少2% | B. | 增加2% | C. | 减少0.2% | D. | 增加0.2% |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将一块正方形铁片的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,已知盒子的容积为300cm3.若设原铁片的边长为xcm,则根据题意可得关于x的方程(x-3×2)(x-3×2)×3=300.
如图,将一块正方形铁片的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,已知盒子的容积为300cm3.若设原铁片的边长为xcm,则根据题意可得关于x的方程(x-3×2)(x-3×2)×3=300.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
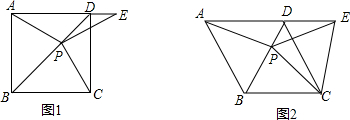
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
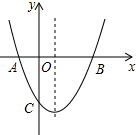 如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,点P是抛物线上的一个动点,连接PA、PB,当S△PAB=8时,点P的坐标为(1+2$\sqrt{2}$,4)或(1-2$\sqrt{2}$,4)或(1,-4).
如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,点P是抛物线上的一个动点,连接PA、PB,当S△PAB=8时,点P的坐标为(1+2$\sqrt{2}$,4)或(1-2$\sqrt{2}$,4)或(1,-4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com