
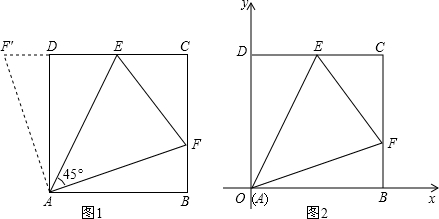
���� ��1���ӳ�EDF�䣬ʹDF��=BF����ABCDΪ�����Σ����������ε���������ȵõ�AB=AD����ABF=��ADF��=90�㣬����SAS�ɵó�������ABF��������ADF��ȫ�ȣ�����ȫ�������ε����ʵõ�AF=AF�䣬��BAF=��DAF�䣬�ɡ�EAFΪ45�㣬�õ���DAE+��FAB=45�㣬���������ɵó���EAF��=45�㣬Ȼ������SAS�õ�������AEF��������AEF�䣬����ȫ�������εĶ�Ӧ����ȵõ�EF=EF�䣬��EF��=ED+DF�䣬�ٽ�DF�任ΪBF���ɵ�֤��
��2����BF=a����CB-FB��ʾ��CF����EF=ED+FB��ʾ��EF����ֱ��������CEF�У����ù��ɶ����г�����a�ķ��̣�������̵Ľ�õ�a��ֵΪ10���ɵó�FΪBC�����ȷֵ㣻
��3����CE=CFʱ��EF��̣���ʱ��CEFΪ����ֱ�������Σ����������F��30��b������FB=b����CB-FB��ʾ��CF����ΪCE����EF=BF+DE=2BF=2b����ֱ��������CEF�У��ɱ�ʾ����CF��CE���ù��ɶ�����ʾ��EF�����г�����b�ķ��̣�������̵Ľ�õ�b��ֵ��ȷ����E��F�����꣬��ֱ��EF�Ľ���ʽΪy=kx+b����E��F���������õ�����k��b�Ķ�Ԫһ�η����飬���������Ľ�õ�k��b��ֵ������ȷ����ֱ��EF�Ľ���ʽ��
��� �⣺��1����ͼ1���ӳ�ED��F�䣬ʹDF��=BF��
���ı���ABCD�������Σ�
��AB=AD����ABF=��ADF��=90�㣬
���ABF�ա�ADF����SAS����
��AF=AF�䣬��BAF=��DAF�䣬
�ߡ�F��AE=��F��AD+��DAE=��BAF+��DAE=��DAB-��EAF=45�㣬
�֡ߡ�EAF=45�㣬
���F��AE=��EAF��
���ڡ�AEF�͡�AEF���У�$\left\{\begin{array}{l}{AF=AF��}\\{��EAF=��EAF��}\\{AE=AE}\end{array}\right.$��
���AEF�ա�AEF�䣨SAS����
��EF=EF��=ED+DF��=ED+BF��
��2����BF=a����CF=30-a��EF=ED+FB=15+a��
����Rt��CEF�У����ݹ��ɶ����ã�EC2+CF2=EF2��
��152+��30-a��2=��15+a��2��
��a=10��
��FΪBC�����ȷֵ㣬
��F��30��10����
��3����CE=CFʱ��EF��̣���ʱ��CEFΪ����ֱ�������Σ�
��F����Ϊ��30��b�����ɵ�FB=b����CF=CE=BC-FB=30-b��
��EF=$\sqrt{2}$��30-b����
�֡�EF=FB+DE��
��$\sqrt{2}$��30-b��=2b����ã�b=$\frac{30\sqrt{2}}{2+\sqrt{2}}$=30$\sqrt{2}$-30��
��FB=DE=30$\sqrt{2}$-30��
��E��30$\sqrt{2}$-30��30����F��30��30$\sqrt{2}$-30����
��ֱ��EF�Ľ���ʽΪy=kx+b��
�߽�E��F���������ã�$\left\{\begin{array}{l}{��30\sqrt{2}-30��k+b=30}\\{30k+b=30\sqrt{2}-30}\end{array}\right.$����ã�$\left\{\begin{array}{l}{k=-1}\\{b=30\sqrt{2}}\end{array}\right.$��
��ֱ��EF�Ľ���ʽΪy=-x+30$\sqrt{2}$��
���� ���⿼����һ�κ����ۺ��⣬�漰��֪ʶ�У�ȫ�������ε��ж������ʣ�������ͼ�����ʣ����ô���ϵ������һ�κ�������ʽ�������ε����ʣ�����ֱ�������ε����ʣ��Լ����ɶ�����������ת������ѧ˼�룬���и�������õ���CE=CFʱ��EF����ǽ�����ʵĹؼ���


 �¿α�ͬ��ѵ��ϵ�д�
�¿α�ͬ��ѵ��ϵ�д� һ����ʦ����Ӧ����������һ��ȫϵ�д�
һ����ʦ����Ӧ����������һ��ȫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2017 | B�� | 2017 | C�� | -$\frac{1}{2017}$ | D�� | $\frac{1}{2017}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
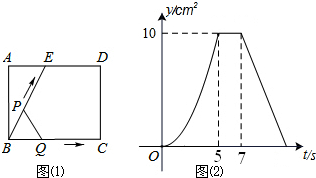 ��ͼ��1����ʾ��EΪ����ABCD�ı�AD��һ�㣬����P��Qͬʱ�ӵ�B��������P������BE-ED-DC�˶�����Cʱֹͣ����Q��BC�˶�����Cʱֹͣ�������˶����ٶȶ���1cm/�룬��P��Qͬʱ����t��ʱ����BPQ�����Ϊycm2����֪y��t�ĺ�����ϵͼ����ͼ��2������t=$\frac{29}{4}$��ʱ����ABE���BQP���ƣ�
��ͼ��1����ʾ��EΪ����ABCD�ı�AD��һ�㣬����P��Qͬʱ�ӵ�B��������P������BE-ED-DC�˶�����Cʱֹͣ����Q��BC�˶�����Cʱֹͣ�������˶����ٶȶ���1cm/�룬��P��Qͬʱ����t��ʱ����BPQ�����Ϊycm2����֪y��t�ĺ�����ϵͼ����ͼ��2������t=$\frac{29}{4}$��ʱ����ABE���BQP���ƣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
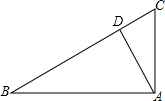 ��ͼ���ڡ�ABC�У���BAC=90�㣬��B=30�㣬AC=5cm��AD��BC��D����BD=��������
��ͼ���ڡ�ABC�У���BAC=90�㣬��B=30�㣬AC=5cm��AD��BC��D����BD=��������| A�� | 10cm | B�� | 7.5cm | C�� | 8.5cm | D�� | 6.5cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
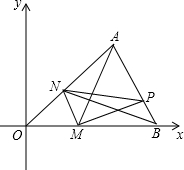 ��ͼ����ƽ��ֱ�������У���AOB���������������ֱ���A��4��4����O��0��0����B��6��0������M������OB�ϵ�һ���㣬����M��MN��AB��MN������OA���ڵ�N��P��AB���ϵ�����㣬����AM��PM��PN��BN�����PMN�����ΪS��
��ͼ����ƽ��ֱ�������У���AOB���������������ֱ���A��4��4����O��0��0����B��6��0������M������OB�ϵ�һ���㣬����M��MN��AB��MN������OA���ڵ�N��P��AB���ϵ�����㣬����AM��PM��PN��BN�����PMN�����ΪS���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com