
分析 (1)过点E作EF∥AB,由平行线的性质可知∠B=∠BEF,∠D=∠DEF,再由角之间的关系即可得出结论;
(2)过点E作EF∥AB,由平行线的性质可知∠B+∠BEF=180°,∠D+∠DEF=180°,再由角之间的关系即可得出结论;
(3)过点E作EF∥AB,由平行线的性质可知∠B=∠BEF,∠D=∠DEF,再由角之间的关系即可得出结论;
(4)过点F作FM∥AB,用(1)的结论可知∠E=∠B+∠EFM,∠G=∠GFM+∠D,再由角之间的关系即可得出结论.
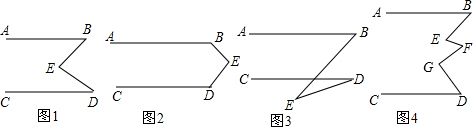
解答 解:(1)相等,过点E作EF∥AB,如图1所示.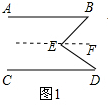
∵EF∥AB,
∴∠B=∠BEF,
∵EF∥AB∥CD,
∴∠D=∠DEF,
∴∠BED=∠BEF+∠DEF=∠B+∠D.
(2)过点E作EF∥AB,如图2所示.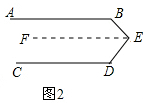
∵AB∥EF,
∴∠B+∠BEF=180°,
∵EF∥AB∥CD,
∴∠D+∠DEF=180°,
∴∠B+∠BEF+∠D+∠DEF=180°+180°,
∵∠E=∠BEF+∠DEF,
∴∠B+∠D+∠E=360°.
(3)过点E作EF∥AB,如图3所示.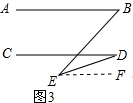
∵AB∥EF,
∴∠B=∠BEF,
∵EF∥AB∥CD,
∴∠D=∠DEF,
∴∠E=∠BEF-∠DEF=∠B-∠D.
(4)过点F作FM∥AB,如图4所示.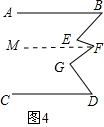
∵AB∥FM,结合(1)结论,
∴∠E=∠B+∠EFM,
∵FM∥AB∥CD,结合(1)结论,
∴∠G=∠GFM+∠D,
又∵∠F=∠EFM+∠GFM,
∴∠E+∠G=∠B+∠D+∠F.
点评 本题考查了平行线的性质以及角的计算,解题的关键是根据平行线的性质得出相等或互补的量.本题属于基础题,难度不大,在计算该题型题目时,根据平行线的性质找出相等(或互补)的角,再根据角与角之间的关系即可得出结论.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:填空题
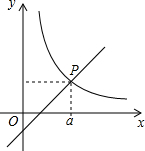 如图,直线y1=x-1与双曲线y2=$\frac{k}{x}$(x>0)交于点P(a,2),则关于x的不等式$\frac{k}{x}$>x-1≥0的解集为1≤x<3.
如图,直线y1=x-1与双曲线y2=$\frac{k}{x}$(x>0)交于点P(a,2),则关于x的不等式$\frac{k}{x}$>x-1≥0的解集为1≤x<3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 减少2% | B. | 增加2% | C. | 减少0.2% | D. | 增加0.2% |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
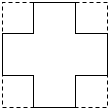 如图,将一块正方形铁片的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,已知盒子的容积为300cm3.若设原铁片的边长为xcm,则根据题意可得关于x的方程(x-3×2)(x-3×2)×3=300.
如图,将一块正方形铁片的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,已知盒子的容积为300cm3.若设原铁片的边长为xcm,则根据题意可得关于x的方程(x-3×2)(x-3×2)×3=300.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知多项式A=(x+2)2+x(1-x)-9
已知多项式A=(x+2)2+x(1-x)-9查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com