
【题目】如图,已知抛物线y=ax2+c过点(﹣2,2),(4,5),过定点F(0,2)的直线l:y=kx+2与抛物线交于A、B两点,点B在点A的右侧,过点B作x轴的垂线,垂足为C.
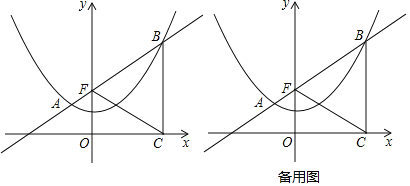
(1)求抛物线的解析式;
(2)当点B在抛物线上运动时,判断线段BF与BC的数量关系 (>、<、=),并证明你的判断;
(3)P为y轴上一点,以B、C、F、P为顶点的四边形是菱形,设点P(0,m),求自然数m的值;
【答案】(1)y=![]() x2+1;(2)=,理由见解析;(3)m的值为6.
x2+1;(2)=,理由见解析;(3)m的值为6.
【解析】
(1)把点(-2,2),(4,5)代入y=ax2+c,即可求解;
(2)设B (x,![]() x2+1),而F(0,2),
x2+1),而F(0,2),
则BF2=x2+(![]() x2+1-2)2=x2+(
x2+1-2)2=x2+(![]() x2-1)2=(
x2-1)2=(![]() x2+1)2,BC=
x2+1)2,BC=![]() x2+1,故BF=BC;
x2+1,故BF=BC;
(3)当m=0时,则四边形BCPF为正方形,此时P点在原点;当点P在F点上方,以B、C、F、P为顶点的四边形是菱形,则CB=CF=PF,则△BCF为等边三角形,CF=2OF=4,PF=CF=4,即可求解.
解:(1)把点(﹣2,2),(4,5)代入y=ax2+c得:![]() ,解得:
,解得:![]() ,
,
所以抛物线解析式为y=![]() x2+1;
x2+1;
(2)设B(x,![]() x2+1),而F(0,2),
x2+1),而F(0,2),
∴BF2=x2+(![]() x2+1﹣2)2=x2+(
x2+1﹣2)2=x2+(![]() x2﹣1)2=(
x2﹣1)2=(![]() x2+1)2,
x2+1)2,
∴BF=![]() x2+1,
x2+1,
∵BC⊥x轴,
∴BC=![]() x2+1,
x2+1,
∴BF=BC,
答案为:=
(3)如图,m为自然数,
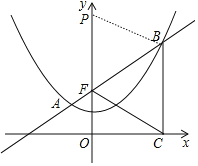
①当点P在F点上方,
∵以B、C、F、P为顶点的四边形是菱形,
∴CB=CF=PF,
而CB=FB,
∴BC=CF=BF,
∴△BCF为等边三角形,
∴∠BCF=60°,
∴∠OCF=30°,
在Rt△OCF中,CF=2OF=4,
∴PF=CF=4,
∴P(0,6);
②当点P在点F下方时,
PF=BC=4,而OF=2,
则OP=2,故m=﹣2(舍去);
③当m=0时,
FP=2,但是BC=4,故不符合要求;
综上,自然数m的值为6.


科目:初中数学 来源: 题型:
【题目】在歌唱比赛中,一位歌手分别转动如下的两个转盘(每个转盘都被分成3等份)一次,根据指针指向的歌曲名演唱两首曲目.

(1)转动转盘①时,该转盘指针指向歌曲“3”的概率是 ;
(2)若允许该歌手替换他最不擅长的歌曲“3”,即指针指向歌曲“3”时,该歌手就选择自己最擅长的歌曲“1”, 请用树形图或列表法中的一种,求他演唱歌曲“1”和“4”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣3,顶点为E,该抛物线与x轴交于A,B两点,与y轴交子点C,且OB=OC=3OA,直线y=﹣![]() x+1与y轴交于点D.求∠DBC﹣∠CBE=_____.
x+1与y轴交于点D.求∠DBC﹣∠CBE=_____.
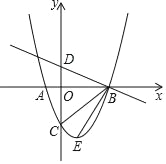
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,BA=BC,∠ABC=90°,点D在AC上,将△ABD绕点B沿顺时针方向旋转90°后,得到△CBE.
(1)求∠DCE的度数;
(2)若AB=4,CD=3AD,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,在△ABC中,点O是AC上一点,过点O的直线与AB,BC的延长线分别相交于点M,N.
【问题引入】
(1)若点O是AC的中点, ![]() ,求
,求![]() 的值;
的值;
温馨提示:过点A作MN的平行线交BN的延长线于点G.
【探索研究】
(2)若点O是AC上任意一点(不与A,C重合),求证: ![]() ;
;
【拓展应用】
(3)如图②所示,点P是△ABC内任意一点,射线AP,BP,CP分别交BC,AC,AB于点D,E,F.若![]() ,
, ![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC内接于⊙O,AD为O的直径交线段BC于点M,DE∥BC,交AB的延长线于点E.
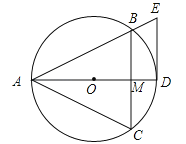
(1)求证:DE是⊙O的切线;
(2)若等边△ABC的边长为6,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com