
【题目】定义:若A,B,C为数轴上三点,若点C到点A的距离是点C到点B的距离2倍,我们就称点C是(A,B)的美好点.
例如:如图1,点A表示的数为![]() ,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的美好点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的美好点,但点D是(B,A)的美好点.
,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的美好点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的美好点,但点D是(B,A)的美好点.

如图2,M,N为数轴上两点,点M所表示的数为![]() ,点N所表示的数为2.
,点N所表示的数为2.

图2
(1)点E,F,G表示的数分别是![]() ,6.5,11,其中是(M,N)美好点的是 ;写出(N,M)美好点H所表示的数是 .
,6.5,11,其中是(M,N)美好点的是 ;写出(N,M)美好点H所表示的数是 .
(2)现有一只电子蚂蚁P从点N开始出发,以2个单位每秒的速度向左运动. 当t为何值时,P,M和N中恰有一个点为其余两点的美好点?
备图
【答案】(1)G,-4或-16(2)1.5、3、9、13.5、6.75、2.25
【解析】
(1)根据美好点的计算方法计算出【M,N】、【N,M】的美好点即可;(2)根据P、M分别为美好点的情况求出t的值即可.
(1)设【M,N】的美好点为x,有两种情况:
当x在M、N之间时,x-(-7)=2(2-x),
解得:x=-1,
当x在N点右边时,x-(-7)=2(x-2),
解得:x=11,
所以E、F、G三点中G点是【M,N】的美好点,
同理可得【N,M】的美好点为:-4或-16,
故答案为:G;-4或-16;
(2)①P为【M,N】的美好点,且点P在M、N之间,
则MP=2NP,点P对应的数是2-3=-1,
所以t=3![]() 2=1.5秒,
2=1.5秒,
②P为【N,M】的美好点,且P在M、N之间,
则NP=2MP,点P对应的数是2-6=-4,
所以t=6![]() 2=3秒,
2=3秒,
③P为【N,M】的美好点,且P在M的左边,
则PN=2PM,PN=18,点P对应的数为2-18=-16,
所以t=18![]() 2=9秒,
2=9秒,
④M为【P,N】的美好点,且点P在M的左边,
则MP=2MN,NP=27,点P对应的数是2-27=-25,
所以t=27![]() 2=13.5秒,
2=13.5秒,
⑤M为【N,P】的美好点,且P在M左边,
则MN=2MP,NP=13.5,点P对应的数为2-13.5=-11.5,
所以t=13.5![]() 2=6.75秒,
2=6.75秒,
⑥M为【N,P】的美好点,且P在M、N之间,
则MN=2MP,NP=4.5,点P对应的数为2-4.5=-2.5,
所以t=4.5![]() 2=2.25秒,
2=2.25秒,
⑦N为【M,P】的美好点,且P在MN之间,
与⑥的情况一致,t=2.25秒,
⑧N为【P,M】的美好点,且P在M的左边,
与③的情况一致,t=9秒,
综上所述:t的值为1.5秒;2.25秒;3秒;6.75秒;9秒;13.5秒时P,M和N中恰有一个点为其余两点的美好点.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
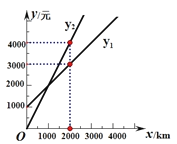
【题目】某单位急需用车,但不准备买车,他们准备和一个体车主或一国营出租车公司中的一家签订合同,设汽车每月行驶x km,应付给个体车主的月租费是y1元,应付给国营出租车公司的月租费是y2元, y1, y2分别与x之间的函数关系的图象(两条射线)如图所示,观察图象,回答下列问题.
(1)分别写出y1, y2与x之间的函数关系式;
(2)每月行驶的路程在什么范围内时,租国营公司的车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a+b=2,则称a与b是关于1的平衡数.
(1)3与 是关于1的平衡数,5﹣![]() 与 是关于1的平衡数;
与 是关于1的平衡数;
(2)若(m+![]() )×(1﹣
)×(1﹣![]() )=﹣5+3
)=﹣5+3![]() ,判断m+
,判断m+![]() 与5﹣
与5﹣![]() 是否是关于1的平衡数,并说明理由.
是否是关于1的平衡数,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图为歌神KTV的两种计费方案说明.若晓莉和朋友们打算在此KTV的一间包厢里连续欢唱6小时,经服务生计算后,告知他们选择包厢计费方案付费会比人数计费方案更便宜,则他们在同一间包厢里欢唱的至少有( )
歌神KTV 包厢计费方案: 包厢每间每小时900元, 每人需另付入场费99元. |
人数计费方案: 每人欢唱3小时540元, 续唱每人每小时80元. |
A.6人B.7人C.8人D.9人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=ax+b与直线y=x+c的交点的横坐标为1,根据图象有下列四个结论:①a<0;②c>0;③对于直线y=x+c上任意两点A(xA,yA)、B(xB,yB),若xA<xB,则yA>yB;④x>1是不等式ax+b<x+c的解集,其中正确的结论是( )
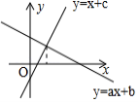
A. ①②B. ①③C. ①④D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=-x2+2(m-1)x+2m-m2的图象关于y轴对称,其顶点为A,与x轴两交点为B,C(B点在C点左侧).
(1)求B,C两点的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为开展“校园读书活动”,雅礼中学读书会计划采购数学文化和文学名著两类书籍共100本. 经了解,购买20 本数学文化和50本文学名著共需1700元, 30本数学文化比30本文学名著贵450 元. (注:所采购的同类书籍价格都一样)
(1)求每本数学文化和文学名著的价格;
(2)若校园读书会要求购买数学文化本数不少于文学名著,且总费用不超过2780元,请求出所有符合条件的购书方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
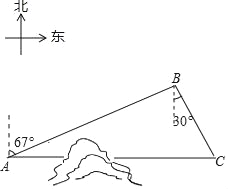
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需要绕行B地,已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长(结果保留整数)
(参考数据:sin67°≈0.92;cos67°≈0.38;![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一对数,如下表,第![]() 个数比第n个数大2(其中n是正整数)
个数比第n个数大2(其中n是正整数)
第1个 | 第2个 | 第3个 | 第4个 | 第5个 | …… |
a | b | c |
(1)第5个数表示为______;第7个数表示为_______.
(2)若第10个数是5,第11个数是8,第12个数为9,则a=______,b=_____,c=______.
(3)第2019个数可表示为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com