Question

【题目】如图，在一个由4×4个小正方形组成的正方形网格中，阴影部分面积与正方形ABCD的面积比是（ ）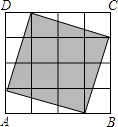

A.5：8
B.3：4
C.9：16
D.1：2

Answer 1

【答案】A
【解析】解：方法1：利用割补法可看出阴影部分的面积是10个小正方形组成的，

所以阴影部分面积与正方形ABCD的面积比是10：16=5：8；

方法2： = ，（ ）2：42=10：16=5：8．

所以答案是：A．

【考点精析】本题主要考查了勾股定理的概念和正方形的性质的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题．