
【题目】某公司有某种海产品2104千克,寻求合适价格,进行8天试销,情况如下:
第几天 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
销售价格(元/千克) | 400 | A | 250 | 240 | 200 | 150 | 125 | 120 |
销售量(千克) | 30 | 40 | 48 | B | 60 | 80 | 96 | 100 |
观察表中数据,发现可以用某种函数刻画这种海产品的每天销售量y(千克)与销售价格x(元/千克)之间的关系. 现假设这批海产品的销售中,每天销售量y(千克)与销售价格x(元/千克)之间都满足这一关系.
(1)猜想函数关系式: . (不必写出自变量的取值)并写出表格中A= ,B= ;
(2)试销8天后,公司决定将售价定为150元/千克. 则余下海产品预计 天可全部售出;
(3)按(2)中价格继续销售15天后,公司发现剩余海产品必须在不超过2天内全部售出,此时需要重新确定一个销售价格,使后面两天都按新价格销售,那么新确定的价格最高不超过多少元/千克才能完成销售任务?
【答案】(1)y=![]() ,A=300,B=50;(2)余下的这些海产品预计再用20天可以全部售出;(3)新确定的价格最高不超过60元/千克才能完成销售任务.
,A=300,B=50;(2)余下的这些海产品预计再用20天可以全部售出;(3)新确定的价格最高不超过60元/千克才能完成销售任务.
【解析】
(1)根据图中数据求出反比例函数,再分别将y=40和x=240代入求出相对应的x和y;
(2)先求出8天销售的总量和剩下的数量m,将x=150代入反比例函数中得到一天的销售量y,![]() 即为所需要的天数;
即为所需要的天数;
(3)求出销售15天后剩余的数量除2得到后两天每天的销售量y,将y的值代入反比例函数中即可求出x.
(1)∵xy=12000,函数解析式为y=![]() ,
,
将y=40和x=240代入上式中求出相对应的x=300和y=50,
∴A=300,B=50;
(2)销售8天后剩下的数量m=2104-(30+40+48+50+60+80+96+100)=1600(千克),
当x=150时,y=![]() =80.
=80.
∴![]() =1600÷80=20(天),
=1600÷80=20(天),
∴余下的这些海产品预计再用20天可以全部售出;
(3)1600-80×15=400(千克),400÷2=200(千克/天),
即如果正好用2天售完,那么每天需要售出200千克.
当y=200时,x=![]() =60.
=60.
所以新确定的价格最高不超过60元/千克才能完成销售任务.


科目:初中数学 来源: 题型:
【题目】如图是一个能自由转动的正六边形转盘,这个转盘被三条分割线分成形状相同,面积相等的三部分,且分别标有“1”、“2”、“3”三个数字,指针的位置固定不动,让转盘自由转动两次,当每次转盘停止后,记录指针指向的数(当指针指向分割线时,视其指向分割线左边的区域),则两次指针指向的数都是奇数的概率为 . 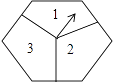
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动阳光体育运动的广泛开展,引导学生走向操场,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了统计图①和图②,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为______,图①中![]() 的值为_____;
的值为_____;
(2)本次调查获取的样本数据的众数为______,中位数为________;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买35号运动鞋多少双?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣ ![]() ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的解析式及A、B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
(3)以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红星中学计划组织“春季研修活动,活动组织负责人从公交公司了解到如下租车信息:
车型 |
|
|
载客量(人/辆) |
|
|
租金(元/辆) |
|
|
校方从实际情况出发,决定租用![]() 、
、![]() 型客车共
型客车共![]() 辆,而且租车费用不超过
辆,而且租车费用不超过![]() 元。
元。
(1)请为校方设计可能的租车方案;
(2)在(1)的条件下,校方根据自愿的原则,统计发现有![]() 人参加,请问校方应如何租车,且又省钱?
人参加,请问校方应如何租车,且又省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种型号热水器的容量为180升,设其工作时间为y分,每分的排水量为x升.
(1)写出y关于x的函数表达式和自变量x的取值范围;
(2)当每分钟的排水量为10升时,热水器工作多长时间?
(3)如果热水器可连续工作的时间不超过1小时,那么每分的排水量应控制在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A. 如果三角形三个角的度数比是3:4:5,那么这个三角形是直角三角形
B. 如果直角三角形两直角边的长分别为a和b,那么斜边的长为a2+b2
C. 若三角形三边长的比为1:2:3,则这个三角形是直角三角形
D. 如果直角三角形两直角边分别为a和b,斜边为c,那么斜边上的高h的长为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图,其对称轴为直线x=1,给出下列结论: ①b2﹣4ac>0;②2a+b=0;③abc>0;④3a+c>0,
则正确的结论个数为( )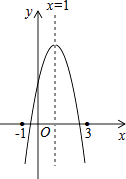
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com