
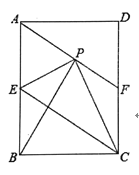
【题目】如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,联结AP并延长AP交CD于F点,
(1)求证:四边形AECF为平行四边形;
(2)如果PA=PC,联结BP,求证:△APB![]() △EPC.
△EPC.
【答案】(1)见解析;(2)见解析.
【解析】
(1)由折叠的性质得到EC垂直平分BP,根据E为AB中点,得到AE=EB,根据EQ为△ABP的中位线,得出AF∥EC即可;
(2)由翻折性质∠EPC=∠EBC=,∠PEC=∠BEC,再求出△AEP为等边三角形即可求解.
解:(1)证明:由折叠得到EC垂直平分BP,
设EC与BP交于Q,∴BQ=EQ
∵E为AB的中点, ∴AE=EB,
∴EQ为△ABP的中位线,∴AF∥EC,
∵AE∥FC, ∴四边形AECF为平行四边形;
(2)∵AF∥EC,∴∠APB=∠EQB=90°
由翻折性质∠EPC=∠EBC=90°,∠PEC=∠BEC
∵E为直角△APB斜边AB的中点,且AP=EP,
∴△AEP为等边三角形 , ∠BAP=∠AEP=60°,
![]()
在△ABP和△EPC中, ∠BAP=∠CEP,∠APB=∠EPC,AP=EP
∴△ABP≌△EPC(AAS),


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】列方程(或方程组)解应用题:
(1)某服装店到厂家选购甲、乙两种服装,若购进甲种服装9件、乙种服装10件,需1810元;购进甲种服装11件乙种服装8件,需1790元,求甲乙两种服装每件价格相差多少元?
(2)某工厂现库存某种原料1200吨,用来生产A、B两种产品,每生产1吨A产品需这种原料2吨、生产费用1000元;每生产1吨B产品需这种原料2.5吨、生产费用900元,如果用来生产这两种产品的资金为53万元,那么A、B两种产品各生产多少吨才能使库存原料和资金恰好用完?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC为等边三角形,点D为直线BC上一动点(点D不与B、C重合).以
AD为边作菱形ADEF,使∠DAF=60°,连接CF.
⑴如图1,当点D在边BC上时,
求证:∠ADB=∠AFC;②请直接判断结论∠AFC=∠ACB+∠DAC是否成立;
⑵如图2,当点D在边BC的延长线上时,其他条件不变,结论∠AFC=∠ACB+∠DAC是否成立?请写出∠AFC、∠ACB、∠DAC之间存在的数量关系,并写出证明过程;
⑶如图3,当点D在边CB的延长线上时,且点A、F分别在直线BC的异侧,其他条件不变,请补全图形,并直接写出∠AFC、∠ACB、∠DAC之间存在的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
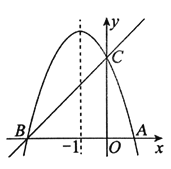
【题目】如图,已知对称轴为直线![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于C点,其中
轴交于C点,其中![]() .
.
(1)求点B的坐标及此抛物线的表达式;
(2)点D为y轴上一点,若直线BD和直线BC的夹角为15,求线段CD的长度;
(3)设点![]() 为抛物线的对称轴
为抛物线的对称轴![]() 上的一个动点,当
上的一个动点,当![]() 为直角三角形时,求点
为直角三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
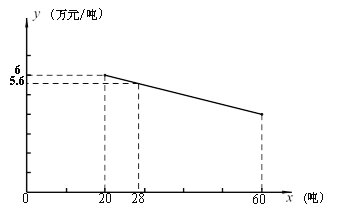
【题目】某工厂生产一种产品,当生产数量至少为20吨,但不超过60吨时,每吨的成本![]() (万元/吨)与生产数量
(万元/吨)与生产数量![]() (吨)之间是一次函数关系,其图像如图所示.
(吨)之间是一次函数关系,其图像如图所示.
(1)求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)如果每吨的成本是4.8万元,求该产品的生产数量;
(3)当生产这种产品的总成本是200万元时,求该产品的生产数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+x+6及一次函数y=﹣x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数(如图所示),请你在图中画出这个新图象,当直线y=﹣x+m与新图象有4个交点时,m的取值范围是( )

A. ﹣![]() <m<3 B. ﹣
<m<3 B. ﹣![]() <m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
<m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
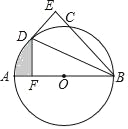
【题目】如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E.
(1)试判断DE与⊙O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F,若BE=3![]() ,DF=3,求图中阴影部分的面积.
,DF=3,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com