
【题目】已知,△ABC为等边三角形,点D为直线BC上一动点(点D不与B、C重合).以
AD为边作菱形ADEF,使∠DAF=60°,连接CF.
⑴如图1,当点D在边BC上时,
求证:∠ADB=∠AFC;②请直接判断结论∠AFC=∠ACB+∠DAC是否成立;
⑵如图2,当点D在边BC的延长线上时,其他条件不变,结论∠AFC=∠ACB+∠DAC是否成立?请写出∠AFC、∠ACB、∠DAC之间存在的数量关系,并写出证明过程;
⑶如图3,当点D在边CB的延长线上时,且点A、F分别在直线BC的异侧,其他条件不变,请补全图形,并直接写出∠AFC、∠ACB、∠DAC之间存在的等量关系.

【答案】⑴①证明:∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°
∵∠DAF=60°
∴∠BAC=∠DAF
∴∠BAD=∠CAF
∵四边形ADEF是菱形,∴AD=AF

∴△ABD≌△ACF
∴∠ADB=∠AFC
②结论:∠AFC=∠ACB+∠DAC成立.
⑵结论∠AFC=∠ACB+∠DAC不成立.
∠AFC、,∠ACB、∠DAC之间的等量关系是
∠AFC=∠ACB-∠DAC(或这个等式的正确变式)
证明:∵△ABC为等边三角形

∴AB=AC
∠BAC=60°
∵∠BAC=∠DAF
∴∠BAD=∠CAF
∵四边形ADEF是菱形
∴AD=AF.
∴△ABD≌△ACF
∴∠ADC=∠AFC
又∵∠ACB=∠ADC+∠DAC,
∴∠AFC=∠ACB-∠DAC
⑶补全图形如下图
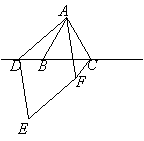
∠AFC、∠ACB、∠DAC之间的等量关系是
∠AFC=2∠ACB-∠DAC
(或∠AFC+∠DAC+∠ACB=180°以及这两个等式的正确变式).
【解析】略


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成任务:
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
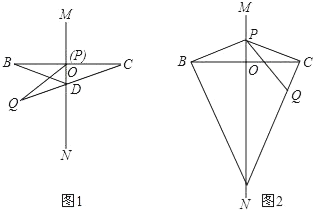
【题目】已知直线MN是线段BC的垂直平分线,垂足为O,P为射线OM上的一点,连接BP,PC.将线段PB绕点P逆时针旋转,得到线段PQ(PQ与PC不重合),旋转角为α(0°<α<180°)直线CQ交MN与点D.
(1)如图1,当α=30°,且点P与点O重合时,∠CDM的度数是 ;
(2)如图2,且点P与点O不重合.
①当α=120°时,求∠CDM的度数;
②用含α的代数式表示∠CDM的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鲜丰水果店计划用![]() 元/盒的进价购进一款水果礼盒以备销售.
元/盒的进价购进一款水果礼盒以备销售.
![]() 据调查,当该种水果礼盒的售价为
据调查,当该种水果礼盒的售价为![]() 元/盒时,月销量为
元/盒时,月销量为![]() 盒,每盒售价每增长
盒,每盒售价每增长![]() 元,月销量就相应减少
元,月销量就相应减少![]() 盒,若使水果礼盒的月销量不低于
盒,若使水果礼盒的月销量不低于![]() 盒,每盒售价应不高于多少元?
盒,每盒售价应不高于多少元?
![]() 在实际销售时,由于天气和运输的原因,每盒水果礼盒的进价提高了
在实际销售时,由于天气和运输的原因,每盒水果礼盒的进价提高了![]() ,而每盒水果礼盒的售价比(1)中最高售价减少了
,而每盒水果礼盒的售价比(1)中最高售价减少了![]() ,月销量比(1)中最低月销量
,月销量比(1)中最低月销量![]() 盒增加了
盒增加了![]() ,结果该月水果店销售该水果礼盒的利润达到了
,结果该月水果店销售该水果礼盒的利润达到了![]() 元,求
元,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
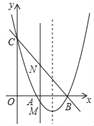
【题目】如图,抛物线y=x2+bx+c与x轴交于点A和B(3,0),与y轴交于点C(0,3).
(1)求抛物线的解析式;
(2)若点M是抛物线上在x轴下方的动点,过M作MN∥y轴交直线BC于点N,求线段MN的最大值;
(3)E是抛物线对称轴上一点,F是抛物线上一点,是否存在以A,B,E,F为顶点的四边形是平行四边形?若存在,请直接写出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
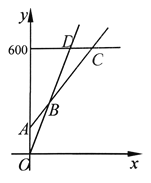
【题目】某乒乓球馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:①金卡售价600元/张,每次凭卡不再收费;②银卡售价150元/张,每次凭卡另收10元;暑期普通票正常出售,两种优惠卡仅限暑期使用,不限次数.设打乒乓x次时,所需总费用为y元.
(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一个坐标系中,若三种消费方式对应的函数图像如图所示,请根据函数图像,写出选择哪种消费方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
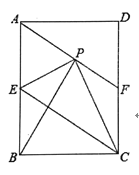
【题目】如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,联结AP并延长AP交CD于F点,
(1)求证:四边形AECF为平行四边形;
(2)如果PA=PC,联结BP,求证:△APB![]() △EPC.
△EPC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】兄弟两人骑马进城,全程51![]() ,马每小时行12
,马每小时行12![]() ,但只能由一个人骑.哥哥每小时步行5
,但只能由一个人骑.哥哥每小时步行5![]() ,弟弟每小时步行4
,弟弟每小时步行4![]() .两人轮换骑马和步行,骑马者走过一段距离就下鞍拴马(下鞍拴马的时间忽略不计),然后独自步行,而步行者到达此地,再上马前进.若他们早上8:00出发,并且同时到达城门,那么他们到达的时间是_____.
.两人轮换骑马和步行,骑马者走过一段距离就下鞍拴马(下鞍拴马的时间忽略不计),然后独自步行,而步行者到达此地,再上马前进.若他们早上8:00出发,并且同时到达城门,那么他们到达的时间是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某省计划5年内全部地级市通高铁.某高铁在泰州境内的建设即将展开,现有大量的沙石需要运输.某车队有载质量为8t、10t的卡车共12辆,全部车辆运输一次能运输100t沙石.
(1)求某车队载质量为8t、10t的卡车各有多少辆;
(2)随着工程的进展,某车队需要一次运输沙石165t以上,为了完成任务,准备新增购这两种卡车共7辆,车队有多少种购买方案?请你一一求出.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com