
����Ŀ����ֱ֪��MN���߶�BC�Ĵ�ֱƽ���ߣ�����ΪO��PΪ����OM�ϵ�һ�㣬����BP��PC�����߶�PB�Ƶ�P��ʱ����ת���õ��߶�PQ��PQ��PC���غϣ�����ת��Ϊ����0�㣼����180�㣩ֱ��CQ��MN���D��
��1����ͼ1��������30�㣬�ҵ�P���O�غ�ʱ����CDM�Ķ������� ����
��2����ͼ2���ҵ�P���O���غϣ�
�ٵ�����120��ʱ�����CDM�Ķ�����
���ú����Ĵ���ʽ��ʾ��CDM�Ķ�����
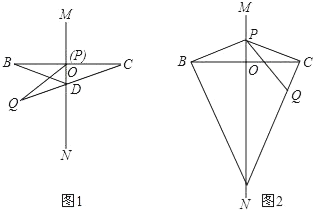
���𰸡���1��75�㣻��2���١�CDM��30�㣬��![]() .
.
��������
��1�����д��ߵ����ʾͿ��Եó�BO=CO������ת�����ʿ��Գ�PQ=OB=PC����������������ڽǵĹ�ϵ�Ϳ��Եó���C=15��������PDC�п��������CDM�Ľ��ۣ�
��2��������ԳƵ����ʿ��Եó���PBD�ա�PCD�����С�PBD=��PCD����PDB=��PDC���Ϳ��Եó���PQC+��PQD=180�����ó���PQD+��PBD=180�������ı��ε��ڽǺ;Ϳ��Եó���BPQ+��BDC=180���������Ϳ��Եó���CDM��ֵ��
������ԳƵ����ʿ��Եó���PBD�ա�PCD�����С�PBD=��PCD����PDB=��PDC���Ϳ��Եó���PQC+��PQD=180�����ó���PQD+��PBD=180�������ı��ε��ڽǺ;Ϳ��Եó���BPQ+��BDC=180���������Ϳ��Եó���CDM=![]() ��180��-a��=90��-
��180��-a��=90��-![]() ��
��
��1����ֱ��MN���߶�BC�Ĵ�ֱƽ���ߣ�
��BO��CO����COD��90����
�߶�PB�Ƶ�P��ʱ����ת���õ��߶�PQ
��PB��PC��PQ��
���Q����C��
�ߡ�Q+��C����BPQ��30����
���C��15����
���C+��CDM��90����
���CDM��75����
��2����ͼ2��
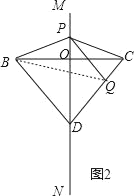
��ֱ��MN���߶�BC�Ĵ�ֱƽ���ߣ�
��PB��PC��BD��CD��
�߶�PB�Ƶ�P��ʱ����ת���õ��߶�PQ
��PB��PC��PQ��
���PQC��PCQ��
����PBD����PCD��
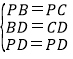 ��
��
���PBD�ա�PCD��SSS����
���PBD����PCD����PDB����PDC��
���PBD����PCD����PQC��
�ߡ�PQC+��PQD��180����
���PQD+��PBD��180����
�ߡ�PBD+��BDQ+��DQP+��BPQ��360����
���BPQ+��BDC��180����
�ߡ�BPQ��120����
���BDC��60����
�ߡ�PDB����PDC��
���PDC��30����
����CDM��30����
��3����ֱ��MN���߶�BC�Ĵ�ֱƽ���ߣ�
��PB��PC��BD��CD��
�߶�PB�Ƶ�P��ʱ����ת���õ��߶�PQ
��PB��PC��PQ��
���PQC��PCQ��
����PBD����PCD��
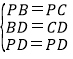 ��
��
���PBD�ա�PCD��SSS����
���PBD����PCD����PDB����PDC��
���PBD����PCD����PQC��
�ߡ�PQC+��PQD��180����
���PQD+��PBD��180����
�ߡ�PBD+��BDQ+��DQP+��BPQ��360����
���BPQ+��BDC��180����
�ߡ�BPQ��a��
���BDC��180����a��
�ߡ�PDB����PDC��
���PDC��90����![]() ��
��
����CDM��90����![]() ��
��


 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д� ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
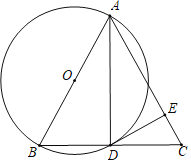
����Ŀ����ͼ����ABC�У�AB=AC��AB�ǡ�O��ֱ����BC���O���ڵ�D����E��AC�ϣ��ҡ�ADE=��B��
��1����֤��DE�ǡ�O�����ߣ�
��2������O�İ뾶Ϊ5��CE=2�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̣����飩��Ӧ���⣺
��1��ij��װ�굽����ѡ���ס������ַ�װ�����������ַ�װ9�������ַ�װ10������1810Ԫ���������ַ�װ11�����ַ�װ8������1790Ԫ����������ַ�װÿ���۸�������Ԫ��
��2��ij�����ֿ��ij��ԭ��1200�֣���������A��B���ֲ�Ʒ��ÿ����1��A��Ʒ������ԭ��2�֡���������1000Ԫ��ÿ����1��B��Ʒ������ԭ��2.5�֡���������900Ԫ������������������ֲ�Ʒ���ʽ�Ϊ53��Ԫ����ôA��B���ֲ�Ʒ���������ٶֲ���ʹ���ԭ�Ϻ��ʽ�ǡ�����ꣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
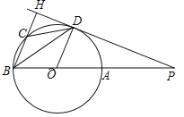
����Ŀ����ͼ����PΪֱ��BA�ӳ�����һ�㣬DΪԲ��һ�㣬BH��PD��H��BDǡ��ƽ�֡�PBH��BH����O��C������CD��OD��
��1����֤��PDΪ��O�����ߣ�
��2����CD=2����ABD=30�������O��ֱ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ΪijУ��������������Զ�ɼ���ͳ��ͼ�������Ҹ������ε�����֮��Ϊ1��2��5��6��4���������Ƶ����12���������������˵��
��һ��������36�������ijɼ���
��������Զ�ɼ�����λ���ֲ���1.8��2.0�飮
��������Զ�ɼ���ƽ����������2.2��
�����������Զ�ɼ�1.85�����£�����1.85��Ϊ���ϸ���ô���ϸ�����Ϊ6�ˣ�
��ȷ���ǣ�������
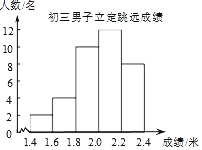
A. �٢�B. �٢�C. �ڢ�D. �ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD��AD=![]() ��������ABCD���Ŷ���B˳ʱ����ת���õ�����EBGF������A��D��C�ֱ����E��F��G��Ӧ����D���F���غϣ��������D��E��F��ͬһ��ֱ���ϣ���ô�߶�DF�ij���____�����ú�
��������ABCD���Ŷ���B˳ʱ����ת���õ�����EBGF������A��D��C�ֱ����E��F��G��Ӧ����D���F���غϣ��������D��E��F��ͬһ��ֱ���ϣ���ô�߶�DF�ij���____�����ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
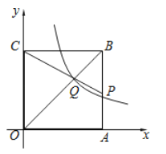
����Ŀ����ͼ�������εı߳�Ϊ![]() �ֱ�λ��
�ֱ�λ��![]() �ᣬ
�ᣬ![]() ���ϣ���
���ϣ���![]() ��
��![]() �ϣ�
�ϣ�![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��ͼ����
��ͼ����![]() ����
����![]() ����
����![]() ��ֵΪ�� ��
��ֵΪ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABCΪ�ȱ������Σ���DΪֱ��BC��һ���㣨��D����B��C�غϣ�����
ADΪ��������ADEF��ʹ��DAF=60��������CF��
����ͼ1������D�ڱ�BC��ʱ��
��֤����ADB=��AFC������ֱ���жϽ�����AFC=��ACB����DAC�Ƿ������
����ͼ2������D�ڱ�BC���ӳ�����ʱ�������������䣬������AFC=��ACB����DAC�Ƿ��������д����AFC����ACB����DAC֮����ڵ�������ϵ����д��֤�����̣�
����ͼ3������D�ڱ�CB���ӳ�����ʱ���ҵ�A��F�ֱ���ֱ��BC����࣬�����������䣬�벹ȫͼ�Σ���ֱ��д����AFC����ACB����DAC֮����ڵĵ�����ϵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
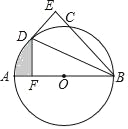
����Ŀ����ͼ��ABΪ��O��ֱ����CΪ��O��һ�㣬��ABC��ƽ���߽���O�ڵ�D��DE��BC�ڵ�E��
��1�����ж�DE���O��λ�ù�ϵ����˵�����ɣ�
��2������D��DF��AB�ڵ�F����BE=3![]() ��DF=3����ͼ����Ӱ���ֵ������
��DF=3����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com