
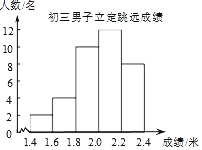
【题目】如图,为某校初三男子立定跳远成绩的统计图,从左到右各分数段的人数之比为1:2:5:6:4,第四组的频数是12,对于下面的四种说法
①一共测试了36名男生的成绩.
②立定跳远成绩的中位数分布在1.8~2.0组.
③立定跳远成绩的平均数不超过2.2.
④如果立定跳远成绩1.85米以下(不含1.85)为不合格,那么不合格人数为6人.
正确的是( )
A. ①③B. ①④C. ②③D. ②④
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形,下列说法正确的是![]()
![]()
A. 任意一个四边形的中点四边形是菱形
B. 任意一个平行四边形的中点四边形是平行四边形
C. 对角线相等的四边形的中点四边形是矩形
D. 对角线垂直的四边形的中点四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016湖南省株洲市)某市对初二综合素质测评中的审美与艺术进行考核,规定如下:考核综合评价得分由测试成绩(满分100分)和平时成绩(满分100分)两部分组成,其中测试成绩占80%,平时成绩占20%,并且当综合评价得分大于或等于80分时,该生综合评价为A等.
(1)孔明同学的测试成绩和平时成绩两项得分之和为185分,而综合评价得分为91分,则孔明同学测试成绩和平时成绩各得多少分?
(2)某同学测试成绩为70分,他的综合评价得分有可能达到A等吗?为什么?
(3)如果一个同学综合评价要达到A等,他的测试成绩至少要多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
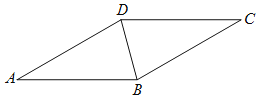
【题目】如图,BD是菱形ABCD的对角线.
(1)请用直尺和圆规作AB的垂直平分线EF,垂足为点E,交AD于点F;(不要求写作法,保留作图痕迹)
(2)在(1)的条件下,连接BF,若∠CBD=75°,求∠DBF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
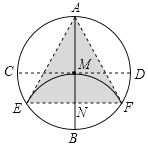
【题目】李老师是我区“IDJP”课题研究的主要成员之一,一天他在视频微课中提出了以下问题:如图,AB,CD为圆形纸片中两条互相垂直的直径,将圆形纸片沿EF折叠,使B与圆心M重合,折痕EF与AB相交于N连结AE,AF.李老师提出两个猜想和一个问题,请你证明或解答出来:
①四边形MEBF是菱形;
②△AEF为等边三角形;
③求S△AEF:S圆.
查看答案和解析>>
科目:初中数学 来源: 题型:
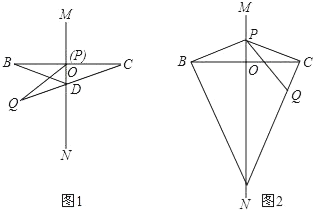
【题目】已知直线MN是线段BC的垂直平分线,垂足为O,P为射线OM上的一点,连接BP,PC.将线段PB绕点P逆时针旋转,得到线段PQ(PQ与PC不重合),旋转角为α(0°<α<180°)直线CQ交MN与点D.
(1)如图1,当α=30°,且点P与点O重合时,∠CDM的度数是 ;
(2)如图2,且点P与点O不重合.
①当α=120°时,求∠CDM的度数;
②用含α的代数式表示∠CDM的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
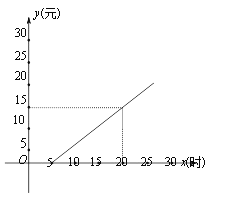
【题目】E-learning即为在线学习,是一种新型的学习方式.某网站提供了A、B两种在线学习的收费方式.A种:在线学习10小时(包括10小时)以内,收取费用5元,超过10小时时,在收取5元的基础上,超过部分每小时收费0.6元(不足1小时按1小时计);B种:每月的收费金额![]() (元)与在线学习时间是
(元)与在线学习时间是![]() (时)之间的函数关系如图所示.
(时)之间的函数关系如图所示.
(1)按照B种方式收费,当![]() 时,求
时,求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(2)如果小明三月份在这个网站在线学习,他按照A种方式支付了20元,那么在线学习的时间最多是多少小时?如果该月他按照B 种方式付费,那么他需要多付多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
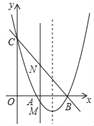
【题目】如图,抛物线y=x2+bx+c与x轴交于点A和B(3,0),与y轴交于点C(0,3).
(1)求抛物线的解析式;
(2)若点M是抛物线上在x轴下方的动点,过M作MN∥y轴交直线BC于点N,求线段MN的最大值;
(3)E是抛物线对称轴上一点,F是抛物线上一点,是否存在以A,B,E,F为顶点的四边形是平行四边形?若存在,请直接写出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①BE⊥AC;②EG=EF;③△EFG≌△GBE;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的个数是( )
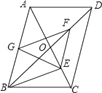
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com