【题目】我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形，下列说法正确的是
A. 任意一个四边形的中点四边形是菱形
B. 任意一个平行四边形的中点四边形是平行四边形
C. 对角线相等的四边形的中点四边形是矩形
D. 对角线垂直的四边形的中点四边形是正方形
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】某游乐园有一个直径为16米的圆形喷水池，喷水池的周边有一圈喷水头，喷出的水柱为抛物线，在距水池中心3米处达到最高，高度为5米，且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合．如图所示，以水平方向为x轴，喷水池中心为原点建立直角坐标系．
（1）求水柱所在抛物线（第一象限部分）的函数表达式；
（2）王师傅在喷水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心多少米以内？
（3）经检修评估，游乐园决定对喷水设施做如下设计改进：在喷出水柱的形状不变的前提下，把水池的直径扩大到32米，各方向喷出的水柱仍在喷水池中心保留的原装饰物（高度不变）处汇合，请探究扩建改造后喷水池水柱的最大高度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线
经过A（2，0）． 设顶点为点P，与x轴的另一交点为点B．
（1）求b的值，求出点P、点B的坐标；
（2）如图，在直线 
上是否存在点D，使四边形OPBD为平行四边形？若存在，求出点D的坐
标；若不存在，请说明理由；
（3）在x轴下方的抛物线上是否存在点M，使△AMP≌△AMB？如果存在，试举例验证你的猜想；如果不存在，试说明理由．
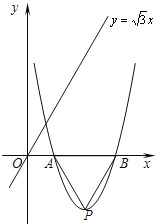
查看答案和解析>>
科目：初中数学 来源： 题型：
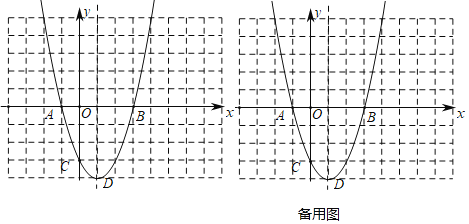
【题目】抛物线y=x2+bx+c与x轴分别交于点A．B，与y轴交于点C，A点坐标为（-1，0），B点坐标为（3，0），顶点为D．
（1）求抛物线解析式；
（2）若点M在抛物线的对称轴上，求△ACM周长的最小值；
（3）以点P为圆心的圆经过A、B两点，且与直线CD相切，求点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某文具店购进A，B两种钢笔，若购进A种钢笔2支，B种钢笔3支，共需90元；购进A种钢笔3支，B种钢笔5支，共需145元．
（1）求该文具店购进A、B两种钢笔每支各多少元？
（2）经统计，B种钢笔售价为30元时，每月可卖64支；每涨价3元，每月将少卖12支，求该文具店B种钢笔销售单价定为多少元时，每月获利最大？最大利润是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
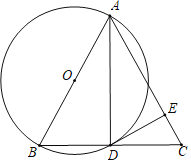
【题目】如图，△ABC中，AB=AC，AB是⊙O的直径，BC与⊙O交于点D，点E在AC上，且∠ADE=∠B．
（1）求证：DE是⊙O的切线；
（2）若⊙O的半径为5，CE=2，求△ABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】茶为国饮，茶文化是中国传统文化的重要组成部分，这也带动了茶艺、茶具、茶服等相关文化的延伸及产业的发展，在“春季茶叶节”期间，某茶具店老板购进了
、
两种不同的茶具.若购进种茶具1套和种茶具2套，需要250元；若购进种茶具3套和种茶具4套则需要600元.
（1）、两种茶具每套进价分别为多少元？
（2）由于茶具畅销，老板决定再次购进、两种茶具共80套，茶具工厂对两种类型的茶具进行了价格调整，种茶具的进价比第一次购进时提高了
，种茶具的进价按第一次购进时进价的八折；如果茶具店老板此次用于购进、两种茶具的总费用不超过6240元，则最多可购进种茶具多少套？
（3）若销售一套种茶具，可获利30元，销售一套种茶具可获利20元，在（2）的条件下，如何进货可使再次购进的茶具获得最大的利润？最大的利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法错误的是
A. Rt△ABC中，AB=3，BC=4，则AC=5；
B. 极差能反映一组数据的变化范围；
C. 经过点A（2，3）的双曲线一定经过点B（-3，-2）；
D. 连接菱形各边中点所得的四边形是矩形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，为某校初三男子立定跳远成绩的统计图，从左到右各分数段的人数之比为1：2：5：6：4，第四组的频数是12，对于下面的四种说法
①一共测试了36名男生的成绩．
②立定跳远成绩的中位数分布在1.8～2.0组．
③立定跳远成绩的平均数不超过2.2．
④如果立定跳远成绩1.85米以下（不含1.85）为不合格，那么不合格人数为6人．
正确的是（ ）
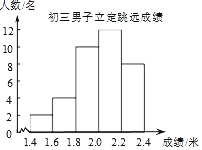
A. ①③B. ①④C. ②③D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
