
【题目】茶为国饮,茶文化是中国传统文化的重要组成部分,这也带动了茶艺、茶具、茶服等相关文化的延伸及产业的发展,在“春季茶叶节”期间,某茶具店老板购进了![]() 、
、![]() 两种不同的茶具.若购进
两种不同的茶具.若购进![]() 种茶具1套和
种茶具1套和![]() 种茶具2套,需要250元;若购进
种茶具2套,需要250元;若购进![]() 种茶具3套和
种茶具3套和![]() 种茶具4套则需要600元.
种茶具4套则需要600元.
(1)![]() 、
、![]() 两种茶具每套进价分别为多少元?
两种茶具每套进价分别为多少元?
(2)由于茶具畅销,老板决定再次购进![]() 、
、![]() 两种茶具共80套,茶具工厂对两种类型的茶具进行了价格调整,
两种茶具共80套,茶具工厂对两种类型的茶具进行了价格调整,![]() 种茶具的进价比第一次购进时提高了
种茶具的进价比第一次购进时提高了![]() ,
,![]() 种茶具的进价按第一次购进时进价的八折;如果茶具店老板此次用于购进
种茶具的进价按第一次购进时进价的八折;如果茶具店老板此次用于购进![]() 、
、![]() 两种茶具的总费用不超过6240元,则最多可购进
两种茶具的总费用不超过6240元,则最多可购进![]() 种茶具多少套?
种茶具多少套?
(3)若销售一套![]() 种茶具,可获利30元,销售一套
种茶具,可获利30元,销售一套![]() 种茶具可获利20元,在(2)的条件下,如何进货可使再次购进的茶具获得最大的利润?最大的利润是多少?
种茶具可获利20元,在(2)的条件下,如何进货可使再次购进的茶具获得最大的利润?最大的利润是多少?
【答案】(1)![]() 种茶具每套进价为100元,
种茶具每套进价为100元,![]() 种茶具每套进价为75元;(2)最多可购进
种茶具每套进价为75元;(2)最多可购进![]() 种茶具30套;(3)再次购进
种茶具30套;(3)再次购进![]() 种茶具30套,
种茶具30套,![]() 种茶具50套可使利润最大,最大利润为1900元
种茶具50套可使利润最大,最大利润为1900元
【解析】
(1)设![]() 种茶具每套进价为
种茶具每套进价为![]() 元,
元,![]() 种茶具每套进价为
种茶具每套进价为![]() 元,根据题目中的等量关系列出方程进而求解即可.
元,根据题目中的等量关系列出方程进而求解即可.
(2)设再次购进![]() 种茶具
种茶具![]() 套,则购进
套,则购进![]() 种茶具
种茶具![]() 套,此次用于购进
套,此次用于购进![]() 、
、![]() 两种茶具的总费用不超过6240元,列出不等式,即可求解.
两种茶具的总费用不超过6240元,列出不等式,即可求解.
(3)设总利润为![]() 元,则
元,则![]() .根据一次函数的性质即可求解.
.根据一次函数的性质即可求解.
(1)设![]() 种茶具每套进价为
种茶具每套进价为![]() 元,
元,![]() 种茶具每套进价为
种茶具每套进价为![]() 元,
元,
![]() 解之得:
解之得:![]() .
.
∴![]() 种茶具每套进价为100元,
种茶具每套进价为100元,![]() 种茶具每套进价为75元.
种茶具每套进价为75元.
(2)设再次购进![]() 种茶具
种茶具![]() 套,则购进
套,则购进![]() 种茶具
种茶具![]() 套,
套,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴最多可购进![]() 种茶具30套.
种茶具30套.
(3)设总利润为![]() 元,则
元,则
![]() .
.
∵![]() ,
,![]() 随
随![]() 的增大而增大,又∵
的增大而增大,又∵![]() ,
,
∴当![]() 时
时![]() 最大
最大![]() (元),
(元),
∴当购进![]() 种茶具30套时,
种茶具30套时,![]() 种茶具的数量:
种茶具的数量:![]() (套),
(套),
∴再次购进![]() 种茶具30套,
种茶具30套,![]() 种茶具50套可使利润最大,最大利润为1900元.
种茶具50套可使利润最大,最大利润为1900元.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
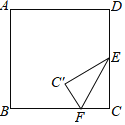
【题目】如图,正方形ABCD的边长是2,点E是CD边的中点,点F是边BC上不与点B,C重合的一个动点,把∠C沿直线EF折叠,使点C落在点C′处.当△ADC′为等腰三角形时,FC的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形,下列说法正确的是![]()
![]()
A. 任意一个四边形的中点四边形是菱形
B. 任意一个平行四边形的中点四边形是平行四边形
C. 对角线相等的四边形的中点四边形是矩形
D. 对角线垂直的四边形的中点四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与x轴交于点
与x轴交于点![]() 、B,与y轴交于点C,对称轴是直线
、B,与y轴交于点C,对称轴是直线![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 如图,求
如图,求![]() 外接圆的圆心M的坐标;
外接圆的圆心M的坐标;
![]() 如图,在BC的另一侧作
如图,在BC的另一侧作![]() ,射线CF交抛物线于点F,求点F的坐标.
,射线CF交抛物线于点F,求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
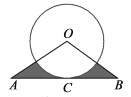
【题目】如图,已知直线AB经过⊙O上的点C,且OA=OB,CA=CB.
(1)求证:直线AB是⊙O的切线;
(2)若∠A=30°,AC=6,求⊙O的周长;
(3)在(2)的条件下,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
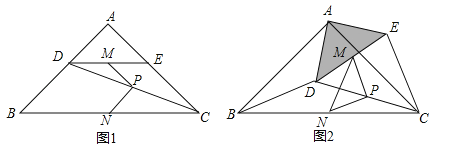
【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016湖南省株洲市)某市对初二综合素质测评中的审美与艺术进行考核,规定如下:考核综合评价得分由测试成绩(满分100分)和平时成绩(满分100分)两部分组成,其中测试成绩占80%,平时成绩占20%,并且当综合评价得分大于或等于80分时,该生综合评价为A等.
(1)孔明同学的测试成绩和平时成绩两项得分之和为185分,而综合评价得分为91分,则孔明同学测试成绩和平时成绩各得多少分?
(2)某同学测试成绩为70分,他的综合评价得分有可能达到A等吗?为什么?
(3)如果一个同学综合评价要达到A等,他的测试成绩至少要多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
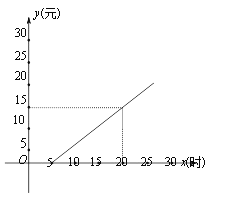
【题目】E-learning即为在线学习,是一种新型的学习方式.某网站提供了A、B两种在线学习的收费方式.A种:在线学习10小时(包括10小时)以内,收取费用5元,超过10小时时,在收取5元的基础上,超过部分每小时收费0.6元(不足1小时按1小时计);B种:每月的收费金额![]() (元)与在线学习时间是
(元)与在线学习时间是![]() (时)之间的函数关系如图所示.
(时)之间的函数关系如图所示.
(1)按照B种方式收费,当![]() 时,求
时,求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(2)如果小明三月份在这个网站在线学习,他按照A种方式支付了20元,那么在线学习的时间最多是多少小时?如果该月他按照B 种方式付费,那么他需要多付多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com