
【题目】(1)计算:-(![]() )-1
)-1![]() +3tan30°-20190+|1-
+3tan30°-20190+|1-![]() |
|
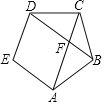
(2)如图,在正五边形ABCDE中,CA与DB相交于点F,若AB=1,求BF.
【答案】(1)-5;(2)BF=![]() .
.
【解析】
(1)根据负指数幂,零指数幂,特殊角的三角函数值,绝对值的性质计算即可.
(2)首先证明AB=AF=1,BF=CF,设BF=CF=x,利用相似三角形的性质,构建方程即可解决问题.
(1)原式=-3-2![]() +
+![]() -1+
-1+![]() -1=-5
-1=-5
(2)在正五边形ABCDE中,∵∠ABC=∠DCB=108°,BC=BA=CD,
∴∠BAC=∠BCA=∠CDB=∠CBD=36°,
∴∠ABF=72°,
∴∠AFB=∠CBD+∠ACB=72°,
∴∠AFB=∠ABF,∠FCB=∠FBC,
∴AF=AB=1,FB=CF,设FB=FC=x,
∵∠BCF=∠BCA,∠CBF=∠CAB,
∴△BCF∽△ACB,
∴CB2=CFCA,
∴x(x+1)=1,
∴x2+x-1=0,
∴x=![]() 或
或![]() (舍弃),
(舍弃),
∴BF=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,E是内心,AE的延长线交△ABC的外接圆于点D,以下四个结论:①BE=AE;②CE⊥AB;③△DEB是等腰三角形;④![]() .其中正确的个数是( )
.其中正确的个数是( )
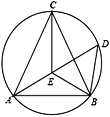
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组为测量一棵古树![]() 和教学楼
和教学楼![]() 的高,先在
的高,先在![]() 处用高1.5米的测角仪测得古树顶端
处用高1.5米的测角仪测得古树顶端![]() 的仰角
的仰角![]() 为
为![]() ,此时教学楼顶端
,此时教学楼顶端![]() 恰好在视线
恰好在视线![]() 上,再向前走9米到达
上,再向前走9米到达![]() 处,又测得教学楼顶端
处,又测得教学楼顶端![]() 的仰角
的仰角![]() 为
为![]() ,点
,点![]() 、
、![]() 、
、![]() 三点在同一水平线上.
三点在同一水平线上.
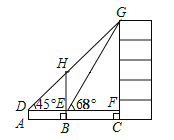
(1)计算古树![]() 的高;
的高;
(2)计算教学楼![]() 的高.(结果精确到0.1米,参考数据:
的高.(结果精确到0.1米,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过A(2,0). 设顶点为点P,与x轴的另一交点为点B.
经过A(2,0). 设顶点为点P,与x轴的另一交点为点B.
(1)求b的值,求出点P、点B的坐标;
(2)如图,在直线 ![]() 上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐
上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐
标;若不存在,请说明理由;
(3)在x轴下方的抛物线上是否存在点M,使△AMP≌△AMB?如果存在,试举例验证你的猜想;如果不存在,试说明理由.
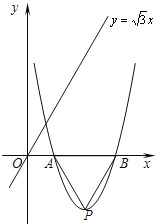
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,求证:BE=AF;
(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
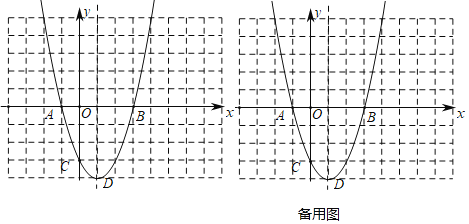
【题目】抛物线y=x2+bx+c与x轴分别交于点A.B,与y轴交于点C,A点坐标为(-1,0),B点坐标为(3,0),顶点为D.
(1)求抛物线解析式;
(2)若点M在抛物线的对称轴上,求△ACM周长的最小值;
(3)以点P为圆心的圆经过A、B两点,且与直线CD相切,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进A,B两种钢笔,若购进A种钢笔2支,B种钢笔3支,共需90元;购进A种钢笔3支,B种钢笔5支,共需145元.
(1)求该文具店购进A、B两种钢笔每支各多少元?
(2)经统计,B种钢笔售价为30元时,每月可卖64支;每涨价3元,每月将少卖12支,求该文具店B种钢笔销售单价定为多少元时,每月获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】茶为国饮,茶文化是中国传统文化的重要组成部分,这也带动了茶艺、茶具、茶服等相关文化的延伸及产业的发展,在“春季茶叶节”期间,某茶具店老板购进了![]() 、
、![]() 两种不同的茶具.若购进
两种不同的茶具.若购进![]() 种茶具1套和
种茶具1套和![]() 种茶具2套,需要250元;若购进
种茶具2套,需要250元;若购进![]() 种茶具3套和
种茶具3套和![]() 种茶具4套则需要600元.
种茶具4套则需要600元.
(1)![]() 、
、![]() 两种茶具每套进价分别为多少元?
两种茶具每套进价分别为多少元?
(2)由于茶具畅销,老板决定再次购进![]() 、
、![]() 两种茶具共80套,茶具工厂对两种类型的茶具进行了价格调整,
两种茶具共80套,茶具工厂对两种类型的茶具进行了价格调整,![]() 种茶具的进价比第一次购进时提高了
种茶具的进价比第一次购进时提高了![]() ,
,![]() 种茶具的进价按第一次购进时进价的八折;如果茶具店老板此次用于购进
种茶具的进价按第一次购进时进价的八折;如果茶具店老板此次用于购进![]() 、
、![]() 两种茶具的总费用不超过6240元,则最多可购进
两种茶具的总费用不超过6240元,则最多可购进![]() 种茶具多少套?
种茶具多少套?
(3)若销售一套![]() 种茶具,可获利30元,销售一套
种茶具,可获利30元,销售一套![]() 种茶具可获利20元,在(2)的条件下,如何进货可使再次购进的茶具获得最大的利润?最大的利润是多少?
种茶具可获利20元,在(2)的条件下,如何进货可使再次购进的茶具获得最大的利润?最大的利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°.
(1)求证:直线AD是⊙O的切线;
(2)若AE⊥BC,垂足为M,⊙O的半径为4,求AE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com