
【题目】如图,正方形ABCD的边长是2,点E是CD边的中点,点F是边BC上不与点B,C重合的一个动点,把∠C沿直线EF折叠,使点C落在点C′处.当△ADC′为等腰三角形时,FC的长为_____.
【答案】![]() 或1.
或1.
【解析】
首先证明DC′≠DA,只要分两种情形讨论即可:①如图1中,当AD=AC′=2时,连接AE.构建方程即可;②如图2中,当点F在BC中点时,易证AC′=DC′,满足条件.
由题意DE=EC=EC′=1,
∴DC′<1+1
∴DC′≠DA,只要分两种情形讨论即可:
①如图1中,当AD=AC′=2时,连接AE.
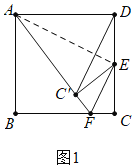
∵AE=AE,AD=AC′,DE=EC′,
∴△ADE≌△AC′E,
∴∠ADE=∠AC′E=90°,
∵∠C=∠FC′E=90°,
∴∠AC′E+∠FC′E=180°,
∴A、C′、F共线,设CF=x,则BF=2-x,AF=2+x,
在Rt△ABF中,22+(2-x)2=(2+x)2,
解得x=![]() .
.
②如图2中,当点F在BC中点时,易证AC′=DC′,满足条件,此时CF=1.
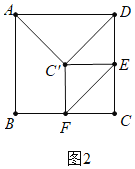
综上所述,满足条件的CF的长为![]() 或1.
或1.
故答案为:![]() 或1.
或1.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
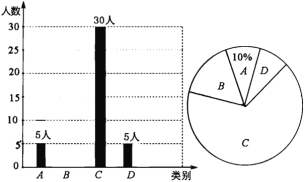
【题目】央视“经典咏流传”开播以来受到社会广泛关注.我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图.请你根据统计图所提供的信息解答下列问题:
图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”.
(1)被调查的总人数是_____________人,扇形统计图中C部分所对应的扇形圆心角的度数为_______.
(2)补全条形统计图;
(3)若该校共有学生1800人,请根据上述调查结果,估计该校学生中A类有__________人;
(4)在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
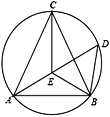
【题目】如图,在△ABC中,AC=BC,E是内心,AE的延长线交△ABC的外接圆于点D,以下四个结论:①BE=AE;②CE⊥AB;③△DEB是等腰三角形;④![]() .其中正确的个数是( )
.其中正确的个数是( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平方向为x轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
(3)经检修评估,游乐园决定对喷水设施做如下设计改进:在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在直角坐标系中,一次函数的图象![]() 与
与![]() 轴交于点
轴交于点![]() ,与一次函数
,与一次函数![]() 的图象
的图象![]() 交于点
交于点![]() .
.
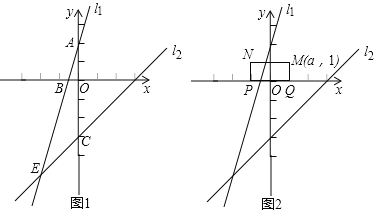
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与y轴交于点
与y轴交于点![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(3)如图2,已知矩形![]() ,
,![]() ,
,![]() ,
,![]() ,矩形
,矩形![]() 的边
的边![]() 在
在![]() 轴上平移,若矩形
轴上平移,若矩形![]() 与直线
与直线![]() 或
或![]() 有交点,直接写出
有交点,直接写出![]() 的取值范围,
的取值范围,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解
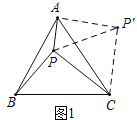
利用旋转变换解决数学问题是一种常用的方法.如图,点![]() 是等边三角形
是等边三角形![]() 内一点,
内一点,![]() ,
,![]() ,
,![]() .求
.求![]() 的度数.
的度数.
为利用已知条件,不妨把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得
得![]() ,连接
,连接![]() ,则
,则![]() 的长为_______;在
的长为_______;在![]() 中,易证
中,易证![]() ,且
,且![]() 的度数为________,综上可得
的度数为________,综上可得![]() 的度数为_______;
的度数为_______;
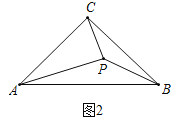
(2)类比迁移
如图,点![]() 是等腰
是等腰![]() 内的一点,
内的一点,![]() ,
,![]() ,
,![]() ,
,![]() .求
.求![]() 的度数;
的度数;
(3)拓展应用
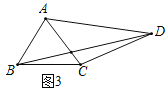
如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,请直接写出
,请直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
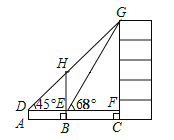
【题目】如图,某数学兴趣小组为测量一棵古树![]() 和教学楼
和教学楼![]() 的高,先在
的高,先在![]() 处用高1.5米的测角仪测得古树顶端
处用高1.5米的测角仪测得古树顶端![]() 的仰角
的仰角![]() 为
为![]() ,此时教学楼顶端
,此时教学楼顶端![]() 恰好在视线
恰好在视线![]() 上,再向前走9米到达
上,再向前走9米到达![]() 处,又测得教学楼顶端
处,又测得教学楼顶端![]() 的仰角
的仰角![]() 为
为![]() ,点
,点![]() 、
、![]() 、
、![]() 三点在同一水平线上.
三点在同一水平线上.
(1)计算古树![]() 的高;
的高;
(2)计算教学楼![]() 的高.(结果精确到0.1米,参考数据:
的高.(结果精确到0.1米,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过A(2,0). 设顶点为点P,与x轴的另一交点为点B.
经过A(2,0). 设顶点为点P,与x轴的另一交点为点B.
(1)求b的值,求出点P、点B的坐标;
(2)如图,在直线 ![]() 上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐
上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐
标;若不存在,请说明理由;
(3)在x轴下方的抛物线上是否存在点M,使△AMP≌△AMB?如果存在,试举例验证你的猜想;如果不存在,试说明理由.
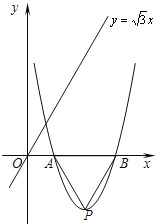
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】茶为国饮,茶文化是中国传统文化的重要组成部分,这也带动了茶艺、茶具、茶服等相关文化的延伸及产业的发展,在“春季茶叶节”期间,某茶具店老板购进了![]() 、
、![]() 两种不同的茶具.若购进
两种不同的茶具.若购进![]() 种茶具1套和
种茶具1套和![]() 种茶具2套,需要250元;若购进
种茶具2套,需要250元;若购进![]() 种茶具3套和
种茶具3套和![]() 种茶具4套则需要600元.
种茶具4套则需要600元.
(1)![]() 、
、![]() 两种茶具每套进价分别为多少元?
两种茶具每套进价分别为多少元?
(2)由于茶具畅销,老板决定再次购进![]() 、
、![]() 两种茶具共80套,茶具工厂对两种类型的茶具进行了价格调整,
两种茶具共80套,茶具工厂对两种类型的茶具进行了价格调整,![]() 种茶具的进价比第一次购进时提高了
种茶具的进价比第一次购进时提高了![]() ,
,![]() 种茶具的进价按第一次购进时进价的八折;如果茶具店老板此次用于购进
种茶具的进价按第一次购进时进价的八折;如果茶具店老板此次用于购进![]() 、
、![]() 两种茶具的总费用不超过6240元,则最多可购进
两种茶具的总费用不超过6240元,则最多可购进![]() 种茶具多少套?
种茶具多少套?
(3)若销售一套![]() 种茶具,可获利30元,销售一套
种茶具,可获利30元,销售一套![]() 种茶具可获利20元,在(2)的条件下,如何进货可使再次购进的茶具获得最大的利润?最大的利润是多少?
种茶具可获利20元,在(2)的条件下,如何进货可使再次购进的茶具获得最大的利润?最大的利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com