
【题目】已知抛物线![]() 与x轴交于点
与x轴交于点![]() 、B,与y轴交于点C,对称轴是直线
、B,与y轴交于点C,对称轴是直线![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 如图,求
如图,求![]() 外接圆的圆心M的坐标;
外接圆的圆心M的坐标;
![]() 如图,在BC的另一侧作
如图,在BC的另一侧作![]() ,射线CF交抛物线于点F,求点F的坐标.
,射线CF交抛物线于点F,求点F的坐标.

【答案】(1)![]() (2)
(2)![]() 点的坐标为
点的坐标为![]() ;(3)
;(3)![]() 点的坐标为
点的坐标为![]()
【解析】
(1)根据抛物线的对称性,结合已知条件求得点B的坐标为![]() ,设抛物线解析式为
,设抛物线解析式为![]() ,整理可得
,整理可得![]() ,所以
,所以![]() ,解得
,解得![]() ,即可求得抛物线解析式为
,即可求得抛物线解析式为![]() ;(2)先求得
;(2)先求得![]() ,由外接圆的圆心M在AB的垂直平分线上,可得
,由外接圆的圆心M在AB的垂直平分线上,可得![]() ,
,![]() ,由两点间的距离公式可得
,由两点间的距离公式可得![]() ,解得
,解得![]() ,即可求得
,即可求得![]() 点的坐标为
点的坐标为![]() ;(3)直线
;(3)直线![]() 交BC于H,延长AH交CF于G,易得
交BC于H,延长AH交CF于G,易得![]() 为等腰直角三角形,所以
为等腰直角三角形,所以![]() ,
,![]() ,再由
,再由![]() 可得
可得![]() ,根据中点坐标公式求得点G的坐标,利用待定系数法求得直线CG的解析式,把直线CG的解析式和抛物线的解析式联立组成方程组,解方程组即可求得点F的坐标.
,根据中点坐标公式求得点G的坐标,利用待定系数法求得直线CG的解析式,把直线CG的解析式和抛物线的解析式联立组成方程组,解方程组即可求得点F的坐标.
解:![]() 抛物线的对称轴为直线
抛物线的对称轴为直线![]() ,
,
![]() 点
点![]() 关于直线
关于直线![]() 的对称点B的坐标为
的对称点B的坐标为![]() ,
,
设抛物线解析式为![]() ,
,
即![]() ,
,
![]() ,解得
,解得![]() ,
,
![]() 抛物线解析式为
抛物线解析式为![]() ;
;
![]() 当
当![]() 时,
时,![]() ,则
,则![]() ,
,
外接圆的圆心M在AB的垂直平分线上,如图1,
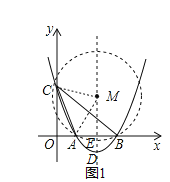
![]() 设
设![]() ,
,
![]() ,
,
![]() ,解得
,解得![]() ,
,
![]() 点的坐标为
点的坐标为![]() ;
;
![]() 直线
直线![]() 交BC于H,延长AH交CF于G,如图2,
交BC于H,延长AH交CF于G,如图2,
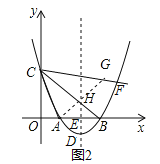
![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,
![]() ,
,
而![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
设直线CG的解析式为![]() ,
,
把![]() ,
,![]() 代入得
代入得![]() ,解得
,解得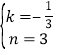 ,
,
![]() 直线CG的解析式为
直线CG的解析式为![]() ,
,
解方程组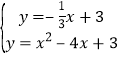 得
得![]() 或
或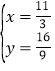 ,
,
![]() 点的坐标为
点的坐标为![]()


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,在直角坐标系中,一次函数的图象![]() 与
与![]() 轴交于点
轴交于点![]() ,与一次函数
,与一次函数![]() 的图象
的图象![]() 交于点
交于点![]() .
.
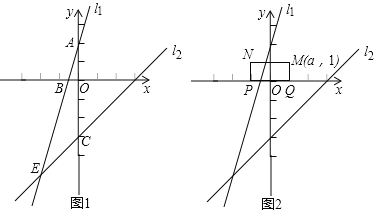
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与y轴交于点
与y轴交于点![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(3)如图2,已知矩形![]() ,
,![]() ,
,![]() ,
,![]() ,矩形
,矩形![]() 的边
的边![]() 在
在![]() 轴上平移,若矩形
轴上平移,若矩形![]() 与直线
与直线![]() 或
或![]() 有交点,直接写出
有交点,直接写出![]() 的取值范围,
的取值范围,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,求证:BE=AF;
(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进A,B两种钢笔,若购进A种钢笔2支,B种钢笔3支,共需90元;购进A种钢笔3支,B种钢笔5支,共需145元.
(1)求该文具店购进A、B两种钢笔每支各多少元?
(2)经统计,B种钢笔售价为30元时,每月可卖64支;每涨价3元,每月将少卖12支,求该文具店B种钢笔销售单价定为多少元时,每月获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
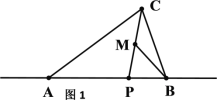
【题目】如图1,在△ABC中,点P为边AB所在直线上一点,连结CP,M为线段CP的中点,若满足∠ACP=∠MBA,则称点P为△ABC的“好点”.
(1)如图2,当∠ABC=90°时,命题“线段AB上不存在“好点”为 (填“真”或“假”)命题,并说明理由;
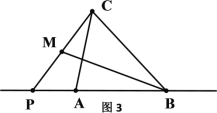
(2)如图3,P是△ABC的BA延长线的一个 “好点”,若PC=4,PB=5,求AP的值;
(3)如图4,在Rt△ABC中,∠CAB=90°,点P是△ABC的“好点”,若AC=4,AB=5,求AP的值.

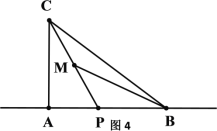
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】茶为国饮,茶文化是中国传统文化的重要组成部分,这也带动了茶艺、茶具、茶服等相关文化的延伸及产业的发展,在“春季茶叶节”期间,某茶具店老板购进了![]() 、
、![]() 两种不同的茶具.若购进
两种不同的茶具.若购进![]() 种茶具1套和
种茶具1套和![]() 种茶具2套,需要250元;若购进
种茶具2套,需要250元;若购进![]() 种茶具3套和
种茶具3套和![]() 种茶具4套则需要600元.
种茶具4套则需要600元.
(1)![]() 、
、![]() 两种茶具每套进价分别为多少元?
两种茶具每套进价分别为多少元?
(2)由于茶具畅销,老板决定再次购进![]() 、
、![]() 两种茶具共80套,茶具工厂对两种类型的茶具进行了价格调整,
两种茶具共80套,茶具工厂对两种类型的茶具进行了价格调整,![]() 种茶具的进价比第一次购进时提高了
种茶具的进价比第一次购进时提高了![]() ,
,![]() 种茶具的进价按第一次购进时进价的八折;如果茶具店老板此次用于购进
种茶具的进价按第一次购进时进价的八折;如果茶具店老板此次用于购进![]() 、
、![]() 两种茶具的总费用不超过6240元,则最多可购进
两种茶具的总费用不超过6240元,则最多可购进![]() 种茶具多少套?
种茶具多少套?
(3)若销售一套![]() 种茶具,可获利30元,销售一套
种茶具,可获利30元,销售一套![]() 种茶具可获利20元,在(2)的条件下,如何进货可使再次购进的茶具获得最大的利润?最大的利润是多少?
种茶具可获利20元,在(2)的条件下,如何进货可使再次购进的茶具获得最大的利润?最大的利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,直线MN与AB、CD分别交于点E、F,FG平分∠EFD,EG⊥FG于点G,若∠CFN=110°,则∠BEG=( )
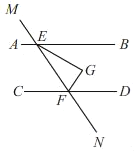
A. 20°B. 25°C. 35°D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某市球类运动协会为了筹备一次大型体育活动,购进了一定数量的体育器材,器材管理员对购买的部分器材进行了统计,表1和图2是器材管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图.请你根据图表中提供的信息,解答以下问题:
频率分布表
器材种类 | 频数 | 频率 |
排 球 | 20 | |
乒乓球拍 | 50 | 0.50 |
篮 球 | 25 | 0.25 |
足 球 | ||
合 计 | 1 |
![]()
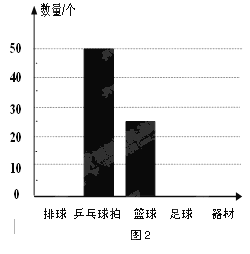
(1)填充图1频率分布表中的空格.
(2)在图2中,将表示“排球”和“足球”的部分补充完整.
(3)已知该协会购买这批体育器材时,篮球和足球一共花去950元,且足球每个的价格比篮球多10元.现准备再采购篮球和足球这两种球共10个(两种球的个数都不能为0),计划资金不超过320元,试问该协会有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校环保小组的同学随机调查了某小区10户家庭一周内使用环保方便袋的数量,数据如下(单位:只):6,5,7,8,7,5,7,10,6,9,利用学过的统计知识,根据上述数据估计该小区200户家庭一周内共需要环保方便袋约( )
A. 200只;B. 1400只;C. 9800只;D. 14000只.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com