
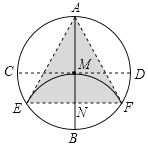
【题目】李老师是我区“IDJP”课题研究的主要成员之一,一天他在视频微课中提出了以下问题:如图,AB,CD为圆形纸片中两条互相垂直的直径,将圆形纸片沿EF折叠,使B与圆心M重合,折痕EF与AB相交于N连结AE,AF.李老师提出两个猜想和一个问题,请你证明或解答出来:
①四边形MEBF是菱形;
②△AEF为等边三角形;
③求S△AEF:S圆.
【答案】(1)见解析;(2)见解析;(3)S△AEF:S圆=3![]() :4π.
:4π.
【解析】
①由折叠的性质可得出BN=MN,∠BNF=∠MNF,结合∠BNF+∠MNF=180°可得出BM⊥EF,由垂径定理可得出EN=FN,由BN,EF互相平分可得出四边形MEBF是平行四边形,再由BN⊥EF可证出四边形MEBF是菱形;
②由菱形的性质可得出∠EBF=∠EMF,由圆周角定理及圆内接四边形的性质可求出∠EAF=60°,由AN=AN,∠ANE=∠ANF,EN=FN可得出△AEN≌△AFN(SAS),利用全等三角形的性质可得出AE=AF,结合∠EAF=60°可证出△AEF为等边三角形;
③设圆M的半径为r,则AN=![]() r,EF=
r,EF=![]() r,利用三角形及圆的面积公式可求出S△AEF,S圆的值,进而可求出S△AEF:S圆的值.
r,利用三角形及圆的面积公式可求出S△AEF,S圆的值,进而可求出S△AEF:S圆的值.
①证明:由折叠的性质可知:BN=MN,∠BNF=∠MNF,
∵∠BNF+∠MNF=180°,
∴∠BNF=90°,即BM⊥EF.
∵点M为圆心,EF为⊙M的弦,BM⊥EF,
∴EN=FN,
∴四边形MEBF为平行四边形,
又∵BN⊥EF,
∴四边形MEBF是菱形;

②证明:由①可知:∠EBF=∠EMF.
∵∠EMF=2∠EAF,∠EBF+∠EAF=180°,
∴∠EAF=60°.
在△AEN和△AFN中,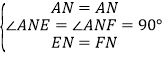 ,
,
∴△AEN≌△AFN(SAS),
∴AE=AF,
∴△AEF为等边三角形;
③解:设圆M的半径为r,则AM=MF=r,MN=![]() r,FN=
r,FN=![]() =
=![]() r,
r,
∴EF=2FN=![]() r,
r,
∴S△AEF=![]() EFAN=
EFAN=![]() r2.
r2.
∴S圆=πr2,
∴S△AEF:S圆=3![]() :4π.
:4π.


科目:初中数学 来源: 题型:
【题目】某文具店购进A,B两种钢笔,若购进A种钢笔2支,B种钢笔3支,共需90元;购进A种钢笔3支,B种钢笔5支,共需145元.
(1)求该文具店购进A、B两种钢笔每支各多少元?
(2)经统计,B种钢笔售价为30元时,每月可卖64支;每涨价3元,每月将少卖12支,求该文具店B种钢笔销售单价定为多少元时,每月获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某市球类运动协会为了筹备一次大型体育活动,购进了一定数量的体育器材,器材管理员对购买的部分器材进行了统计,表1和图2是器材管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图.请你根据图表中提供的信息,解答以下问题:
频率分布表
器材种类 | 频数 | 频率 |
排 球 | 20 | |
乒乓球拍 | 50 | 0.50 |
篮 球 | 25 | 0.25 |
足 球 | ||
合 计 | 1 |
![]()
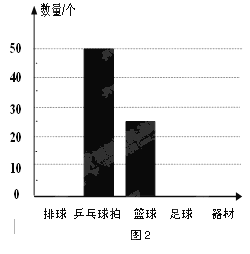
(1)填充图1频率分布表中的空格.
(2)在图2中,将表示“排球”和“足球”的部分补充完整.
(3)已知该协会购买这批体育器材时,篮球和足球一共花去950元,且足球每个的价格比篮球多10元.现准备再采购篮球和足球这两种球共10个(两种球的个数都不能为0),计划资金不超过320元,试问该协会有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°.
(1)求证:直线AD是⊙O的切线;
(2)若AE⊥BC,垂足为M,⊙O的半径为4,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
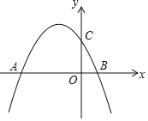
【题目】如图,二次函数Y=-![]() x2-
x2-![]() x+2图象与x轴交于A、B两点,与y轴交于C点,点D(m,n)是抛物线在第二象限的部分上的一动点,则四边形OCDA的面积的最大值是______.
x+2图象与x轴交于A、B两点,与y轴交于C点,点D(m,n)是抛物线在第二象限的部分上的一动点,则四边形OCDA的面积的最大值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
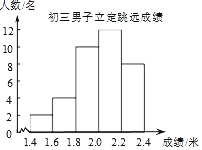
【题目】如图,为某校初三男子立定跳远成绩的统计图,从左到右各分数段的人数之比为1:2:5:6:4,第四组的频数是12,对于下面的四种说法
①一共测试了36名男生的成绩.
②立定跳远成绩的中位数分布在1.8~2.0组.
③立定跳远成绩的平均数不超过2.2.
④如果立定跳远成绩1.85米以下(不含1.85)为不合格,那么不合格人数为6人.
正确的是( )
A. ①③B. ①④C. ②③D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校环保小组的同学随机调查了某小区10户家庭一周内使用环保方便袋的数量,数据如下(单位:只):6,5,7,8,7,5,7,10,6,9,利用学过的统计知识,根据上述数据估计该小区200户家庭一周内共需要环保方便袋约( )
A. 200只;B. 1400只;C. 9800只;D. 14000只.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),交
的左侧),交![]() 轴于点
轴于点![]() ,将直线
,将直线![]() 以点
以点![]() 为旋转中心,顺时针旋
为旋转中心,顺时针旋![]() 转,交
转,交![]() 轴于点
轴于点![]() ,交抛物线于另一点
,交抛物线于另一点![]() .直线
.直线![]() 的解析式为:
的解析式为:![]()

![]() 点
点![]() 是第一象限内抛物线上一点,当
是第一象限内抛物线上一点,当![]() 的面积最大时,在线段
的面积最大时,在线段![]() 上找一点
上找一点![]() (不与
(不与![]() 重合),使
重合),使![]() 的值最小,求出点
的值最小,求出点![]() 的坐标,并直接写出
的坐标,并直接写出![]() 的最小值;
的最小值;
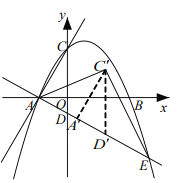
![]() 如图,将
如图,将![]() 沿射线
沿射线![]() 方向以每秒
方向以每秒![]() 个单位的速度平移,记平移后的
个单位的速度平移,记平移后的![]() 为
为![]() ,平移时间为
,平移时间为![]() 秒,当
秒,当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想了解周围的人是否具有节水意识,于是他设计了一份简单的调查问卷,并到小区里随机调查了40人,他将部分调查结果制成了统计图.
小明的调查问卷:
调查问卷
年龄:________岁
(1)你在刷牙时会一直开着水龙头吗?
A.经常这样 B.有时这料 C.从不这样
(2)你会将用过的水另作他用吗?用洗衣服的水拖地、冲厕所等.
A.经常这样 B.有时这料 C.从不这样
小明绘制的统计图:
问题1中各年龄段选择“从不这样”的情况 问题1中各年龄段选择“经常这样”的情况
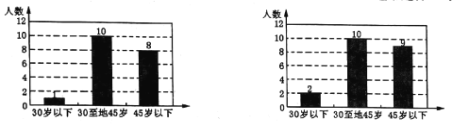
(1)在小明调查的40人中,各年龄段分别有多少人接受了调查?
(2)通过小明的调查数据,你认为哪个年龄段的人最具有节水意识?
(3)为了倡导你身边的人节约用水,你有什么建议?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com