
【题目】如图,二次函数Y=-![]() x2-
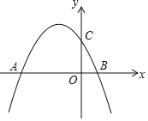
x2-![]() x+2图象与x轴交于A、B两点,与y轴交于C点,点D(m,n)是抛物线在第二象限的部分上的一动点,则四边形OCDA的面积的最大值是______.
x+2图象与x轴交于A、B两点,与y轴交于C点,点D(m,n)是抛物线在第二象限的部分上的一动点,则四边形OCDA的面积的最大值是______.
【答案】8
【解析】
根据解析式求得点A、C坐标,过点D作DH⊥x轴于点H,运用割补法即可得到:四边形OCDA的面积=△ADH的面积+四边形OCDH的面积,据此列式计算化简就可求得S关于m的函数关系,配方成顶点式可得其最值情况.
解:在y=-![]() x2-
x2-![]() x+2中,当x=0时,y=2,
x+2中,当x=0时,y=2,
∴C(0,2),
当y=0时,有-![]() x2-
x2-![]() x+2=0,解得:x=-4或x=1,
x+2=0,解得:x=-4或x=1,
∴点A(-4,0)、B(1,0),
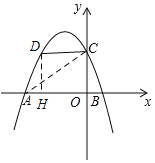
∵点D(m,n)是抛物线在第二象限的部分上的一动点,
∴D(m,-![]() m2-
m2-![]() m+2),
m+2),
过点D作DH⊥x轴于点H,则DH=-![]() m2-
m2-![]() m+2,AH=m+4,HO=-m,
m+2,AH=m+4,HO=-m,
∵四边形OCDA的面积=△ADH的面积+四边形OCDH的面积,
∴S=![]() (m+4)×(-
(m+4)×(-![]() m2-
m2-![]() m+2)+
m+2)+![]() (-
(-![]() m2-
m2-![]() m+2+2)×(-m),
m+2+2)×(-m),
=-m2-4m+4
=-(m+2)2+8,(-4<m<0);
则m=-2时,S取得最大值,最大值为8,


科目:初中数学 来源: 题型:
【题目】把y=![]() x2的图象向上平移2个单位.
x2的图象向上平移2个单位.
(1)求新图象的解析式、顶点坐标和对称轴;
(2)画出平移后的函数图象;
(3)求平移后的函数的最大值或最小值,并求对应的x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x 2+bx+c与x轴交于A、B两点,与y轴交于点C,已知经过B、C两点的直线的表达式为y=-x+3.
(1)求抛物线的函数表达式;
(2)点P(m,0)是线段OB上的一个动点,过点P作y轴的平行线,交直线BC于D,交抛物线于E,EF∥x轴,交直线BC于F,DG∥x轴,FG∥y轴,DG与FG交于点G.设四边形DEFG的面积为S,当m为何值时S最大,最大值是多少?
(3)在坐标平面内是否存在点Q,将△OAC绕点Q逆时针旋转90°,使得旋转后的三角形恰好有两个顶点落在抛物线上.若存在,求出所有符合条件的点Q的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
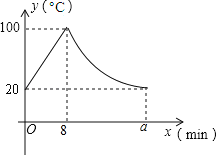
【题目】某小学为每个班级配备了一种可以加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10℃,待加热到100℃,饮水机自动停止加热,水温开始下降,水温y(℃)与通电时间x(min)成反比例关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温为20℃,接通电源后,水温y(℃)与通电时间x(min)的关系如下图所示,回答下列问题:
(1)当0≤x≤8时,求y与x之间的函数关系式;
(2)求出图中a的值;
(3)某天早上7:20,李老师将放满水后的饮水机电源打开,若他想在8:00上课前能喝到不超过40℃的温开水,问:他应在什么时间段内接水?
查看答案和解析>>
科目:初中数学 来源: 题型:
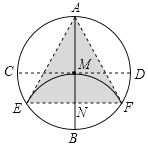
【题目】李老师是我区“IDJP”课题研究的主要成员之一,一天他在视频微课中提出了以下问题:如图,AB,CD为圆形纸片中两条互相垂直的直径,将圆形纸片沿EF折叠,使B与圆心M重合,折痕EF与AB相交于N连结AE,AF.李老师提出两个猜想和一个问题,请你证明或解答出来:
①四边形MEBF是菱形;
②△AEF为等边三角形;
③求S△AEF:S圆.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为推动“时刻听党话 永远跟党走”校园主题教育活动,计划开展四项活动:A:党史演讲比赛,B:党史手抄报比赛,C:党史知识竞赛,D:红色歌咏比赛.校团委对学生最喜欢的一项活动进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2两幅不完整的统计图.请结合图中信息解答下列问题:
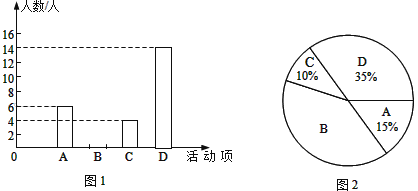
(1)本次共调查了 名学生;
(2)将图1的统计图补充完整;
(3)已知在被调查的最喜欢“党史知识竞赛”项目的4个学生中只有1名女生,现从这4名学生中任意抽取2名学生参加该项目比赛,请用画树状图或列表的方法,求出恰好抽到一名男生一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一批货物准备运往某地,有甲、乙、丙三辆卡车可雇用.已知甲、乙、丙三辆车每次运货量不变,且甲、乙两车单独运完这批货物分别用![]() 次;甲、丙两车合运相同次数,运完这批货物,甲车共运
次;甲、丙两车合运相同次数,运完这批货物,甲车共运![]() 吨;乙、丙两车合运相同次数,运完这批货物乙车共运
吨;乙、丙两车合运相同次数,运完这批货物乙车共运![]() 吨,现甲、乙、丙合运相同次数把这批货物运完,货主应付甲车主的运费为___________ 元.(按每吨运费
吨,现甲、乙、丙合运相同次数把这批货物运完,货主应付甲车主的运费为___________ 元.(按每吨运费![]() 元计算)
元计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,则巡逻船从出发到成功拦截捕鱼船所用的时间是( )

A. 1小时 B. 2小时 C. 3小时 D. 4小时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com