
【题目】兄弟两人骑马进城,全程51![]() ,马每小时行12
,马每小时行12![]() ,但只能由一个人骑.哥哥每小时步行5
,但只能由一个人骑.哥哥每小时步行5![]() ,弟弟每小时步行4
,弟弟每小时步行4![]() .两人轮换骑马和步行,骑马者走过一段距离就下鞍拴马(下鞍拴马的时间忽略不计),然后独自步行,而步行者到达此地,再上马前进.若他们早上8:00出发,并且同时到达城门,那么他们到达的时间是_____.
.两人轮换骑马和步行,骑马者走过一段距离就下鞍拴马(下鞍拴马的时间忽略不计),然后独自步行,而步行者到达此地,再上马前进.若他们早上8:00出发,并且同时到达城门,那么他们到达的时间是_____.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
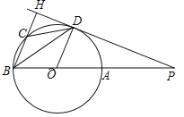
【题目】如图,点P为直径BA延长线上一点,D为圆上一点,BH⊥PD于H,BD恰好平分∠PBH,BH交⊙O于C,连接CD,OD.
(1)求证:PD为⊙O的切线;
(2)若CD=2,∠ABD=30°,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC为等边三角形,点D为直线BC上一动点(点D不与B、C重合).以
AD为边作菱形ADEF,使∠DAF=60°,连接CF.
⑴如图1,当点D在边BC上时,
求证:∠ADB=∠AFC;②请直接判断结论∠AFC=∠ACB+∠DAC是否成立;
⑵如图2,当点D在边BC的延长线上时,其他条件不变,结论∠AFC=∠ACB+∠DAC是否成立?请写出∠AFC、∠ACB、∠DAC之间存在的数量关系,并写出证明过程;
⑶如图3,当点D在边CB的延长线上时,且点A、F分别在直线BC的异侧,其他条件不变,请补全图形,并直接写出∠AFC、∠ACB、∠DAC之间存在的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
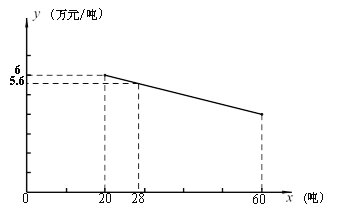
【题目】某工厂生产一种产品,当生产数量至少为20吨,但不超过60吨时,每吨的成本![]() (万元/吨)与生产数量
(万元/吨)与生产数量![]() (吨)之间是一次函数关系,其图像如图所示.
(吨)之间是一次函数关系,其图像如图所示.
(1)求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)如果每吨的成本是4.8万元,求该产品的生产数量;
(3)当生产这种产品的总成本是200万元时,求该产品的生产数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
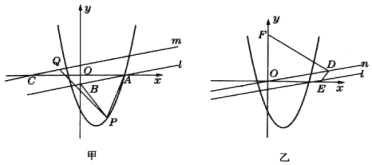
【题目】已知二次函数y=﹣x2+x+6及一次函数y=﹣x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数(如图所示),请你在图中画出这个新图象,当直线y=﹣x+m与新图象有4个交点时,m的取值范围是( )

A. ﹣![]() <m<3 B. ﹣
<m<3 B. ﹣![]() <m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
<m<2 C. ﹣2<m<3 D. ﹣6<m<﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() 点,经过点
点,经过点![]() 的抛物线
的抛物线![]() 上有一动点
上有一动点![]() ,且点
,且点![]() 在直线
在直线![]() 的下方.
的下方.
(1)平移直线![]() 经过点
经过点![]() ,得到直线
,得到直线![]() ,点
,点![]() 为直线
为直线![]() 上一个动点,连接
上一个动点,连接![]() ,当
,当![]() 面积最大时,求
面积最大时,求![]() 的最小值.
的最小值.
(2)平移直线![]() 经过原点,得到直线
经过原点,得到直线![]() ,点
,点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() 点横坐标为6,点
点横坐标为6,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,当
轴上,当![]() 时,抛物线上是否存在点
时,抛物线上是否存在点![]() ,使四边形
,使四边形![]() 是矩形?如果存在,请求出点
是矩形?如果存在,请求出点![]() 的坐标,如果不存在,请说明理由.
的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
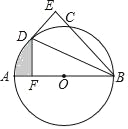
【题目】如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E.
(1)试判断DE与⊙O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F,若BE=3![]() ,DF=3,求图中阴影部分的面积.
,DF=3,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=x2﹣4的图象与x轴交于点A、B(点A位于点B的左侧),C为顶点.一次函数y=mx+2的图象经过点A,与y轴交于点D.
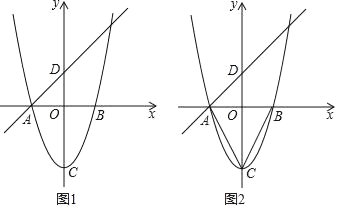
(1)求直线AD的函数表达式;
(2)平移该抛物线得到一条新抛物线,设新抛物线的顶点为C′.若新抛物线的顶点和原抛物线的顶点的连线CC′平行于直线AD,且当1≤x≤3时,新抛物线对应的函数值有最小值为﹣1,求新抛物线对应的函数表达式;
(3)如图,连接AC、BC,在坐标平面内,直接写出使得△ACD与△EBC相似(其中点A与点E是对应点)的点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表显示了同学们用计算机模拟随机投针实验的某次实验的结果.
投针次数n | 1000 | 2000 | 3000 | 4000 | 5000 | 10000 | 20000 |
针与直线相交的次数m | 454 | 970 | 1430 | 1912 | 2386 | 4769 | 9548 |
针与直线相交的频率p=
| 0.454 | 0.485 | 0.4767 | 0.478 | 0.4772 | 0.4769 | 0.4774 |
下面有三个推断:
①投掷1000次时,针与直线相交的次数是454,针与直线相交的概率是0.454;
②随着实验次数的增加,针与直线相交的频率总在0.477附近,显示出一定的稳定性,可以估计针与直线相交的概率是0.477;
③若再次用计算机模拟此实验,则当投掷次数为10000时,针与直线相交的频率一定是0.4769.
其中合理的推断的序号是:_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com