
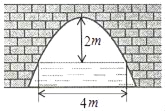
【题目】如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽_____m.
【答案】4![]() .
.
【解析】
根据已知得出直角坐标系,进而求出二次函数解析式,再通过把y=-2代入抛物线解析式得出水面宽度,即可得出答案.
建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,
抛物线以y轴为对称轴,且经过A,B两点,OA和OB可求出为AB的一半2米,抛物线顶点C坐标为(0,2),
通过以上条件可设顶点式y=ax2+2,其中a可通过代入A点坐标(﹣2,0),
到抛物线解析式得出:a=﹣0.5,所以抛物线解析式为y=﹣0.5x2+2,
当水面下降2米,通过抛物线在图上的观察可转化为:
当y=﹣2时,对应的抛物线上两点之间的距离,也就是直线y=﹣2与抛物线相交的两点之间的距离,
可以通过把y=﹣2代入抛物线解析式得出:
﹣2=﹣0.5x2+2,
解得:x=±2![]() ,所以水面宽度增加到4
,所以水面宽度增加到4![]() 米,
米,
故答案为:4![]() .
.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的顶点
的顶点![]() 在坐标原点,正方形
在坐标原点,正方形![]() 的边
的边![]() 与
与![]() 在同一直线上,
在同一直线上, ![]() 与
与![]() 在同一直线上,且
在同一直线上,且![]() ,
,![]() 边和
边和![]() 边所在直线的解析式分别为:
边所在直线的解析式分别为: ![]() 和
和![]() ,则点
,则点![]() 的坐标是( )
的坐标是( )
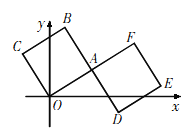
A.(6,-1)B.(7,-1)C.(7,-2)D.(6,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年“双十一”期间,某快递公司计划租用甲、乙两种车辆快递货物,从货物量来计算:若租用两种车辆合运,10天可以完成任务;若单独租用乙种车辆,完成任务的天数是单独租用甲种车辆完成任务天数的2倍.
(1)求甲、乙两种车辆单独完成任务分别需要多少天?
(2)已知租用甲、乙两种车辆合运需租金65000元,甲种车辆每天的租金比乙种车辆每天的租金多1500元,试问:租甲和乙两种车辆、单独租甲种车辆、单独租乙种车辆这三种租车方案中,哪一种租金最少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )

A.带①去B.带②去C.带③去D.带①和②去
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:
(1)计算判断:(计算并判断大小,填写符号:“>”“<”或“=”)
①当![]() ,
,![]() 时,
时,![]() _____
_____![]() ;
;
②当![]() ,
,![]() 时,
时,![]() _____
_____![]() ;
;
③当![]() ,
,![]() 时,
时,![]() ______
______![]() ;
;
④当![]() ,
,![]() 时,
时,![]() ______
______![]() ;
;
⑤当![]() ,
,![]() 时,
时,![]() ______
______![]() ;
;
⑥当![]() ,
,![]() 时,
时,![]() _______
_______![]() ;
;
…
(2)归纳猜想:猜想并写出关于![]() 与
与![]() (
(![]() ,
,![]() 是常数,且
是常数,且![]() ,
,![]() )之间的数量关系;
)之间的数量关系;
(3)探究证明:请补全以下证明过程:
证明:根据一个实数的平方是非负数,可得![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
…
(4)实践应用:要制作面积为![]() 的长方形(或正方形)框架,直接利用探究得出的结论,求出框架周长的最小值.
的长方形(或正方形)框架,直接利用探究得出的结论,求出框架周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,C,为半径是6的⊙O上两点,点B为![]() 的中点,以线段BA,BC为邻边作菱形ABCD,使点D落在⊙O内(不含圆周上),则下列结论:①直线BD必过圆心O;②菱形ABCD的边长a的取值范围是0<a<10;③若点D与圆心O重合,则∠ABC=120°;④若DO=2,则菱形ABCD的边长为
的中点,以线段BA,BC为邻边作菱形ABCD,使点D落在⊙O内(不含圆周上),则下列结论:①直线BD必过圆心O;②菱形ABCD的边长a的取值范围是0<a<10;③若点D与圆心O重合,则∠ABC=120°;④若DO=2,则菱形ABCD的边长为![]() 或
或![]() .其中正确的是( )
.其中正确的是( )
A. ①③ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为丰富综合实践活动,开设了四个实验室如下:A.物理;B.化学;C.信息;D.生物.为了解学生最喜欢哪个实验室,随机抽取了部分学生进行调查,每位被调查的学生都选择了一个自己最喜欢的实验室,调查后将调查结果绘制成了如图统计图,请根据统计图回答下列问题
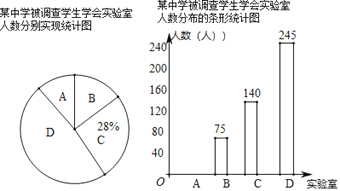
(1)求这次被调查的学生人数.
(2)请将条形统计图补充完整.
(3)求出扇形统计图中B对应的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
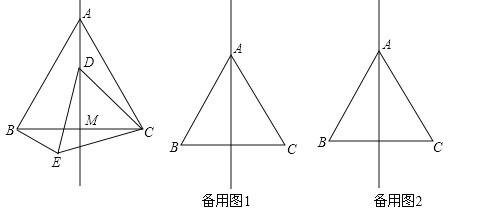
【题目】如图,在等边△ABC中,线段AM为BC边上的中线.动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.
(1)求∠CAM的度数;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
(3)当动D在直线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com