
【题目】综合与探究:
(1)计算判断:(计算并判断大小,填写符号:“>”“<”或“=”)
①当![]() ,
,![]() 时,
时,![]() _____
_____![]() ;
;
②当![]() ,
,![]() 时,
时,![]() _____
_____![]() ;
;
③当![]() ,
,![]() 时,
时,![]() ______
______![]() ;
;
④当![]() ,
,![]() 时,
时,![]() ______
______![]() ;
;
⑤当![]() ,
,![]() 时,
时,![]() ______
______![]() ;
;
⑥当![]() ,
,![]() 时,
时,![]() _______
_______![]() ;
;
…
(2)归纳猜想:猜想并写出关于![]() 与
与![]() (
(![]() ,
,![]() 是常数,且
是常数,且![]() ,
,![]() )之间的数量关系;
)之间的数量关系;
(3)探究证明:请补全以下证明过程:
证明:根据一个实数的平方是非负数,可得![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
…
(4)实践应用:要制作面积为![]() 的长方形(或正方形)框架,直接利用探究得出的结论,求出框架周长的最小值.
的长方形(或正方形)框架,直接利用探究得出的结论,求出框架周长的最小值.
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
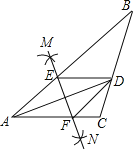
【题目】如图,在![]() 中,AD平分
中,AD平分![]() ,按如下步骤作图:
,按如下步骤作图:
第一步,分别以点A、D为圆心,以大于![]() 的长为半径在AD两侧作弧,交于两点M、N;
的长为半径在AD两侧作弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若![]() ,
,![]() ,
,![]() ,求BD的长是______.
,求BD的长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E是AB的中点,CE和BD交于点O,如△ODC的面积为4,则四边形AEOD的面积是( )
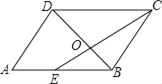
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,如果两个三角形全等,则它们面积相等,而两个不全等的三角形,在某些情况下,可通过证明等底等高来说明它们的面积相等,已知![]() 与
与![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,连接
,连接![]() 、
、![]() .
.
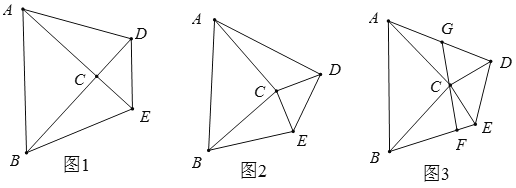
(1)如图1,当![]() 时,求证
时,求证![]()
(2)如图2,当![]() 时,上述结论是否仍然成立?如果成立,请证明;如果不成立,说明理由.
时,上述结论是否仍然成立?如果成立,请证明;如果不成立,说明理由.
(3)如图3,在(2)的基础上,如果![]() 点为
点为![]() 的中点,连接
的中点,连接![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,试猜想
,试猜想![]() 与
与![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多多班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是( )

A.极差是47B.众数是42
C.中位数是58D.每月阅读数量超过40的有4个月
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com