
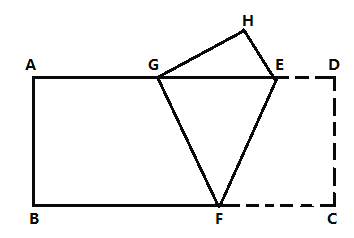
【题目】如图,在长方形纸片![]() 中,
中,![]() ,
,![]() ,拆叠纸片
,拆叠纸片![]() ,使顶点
,使顶点![]() 落在边
落在边![]() 上的点
上的点![]() 处,折痕分别交边
处,折痕分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() ,则
,则![]() 的面积最大值是__________.
的面积最大值是__________.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】综合与探究:
(1)计算判断:(计算并判断大小,填写符号:“>”“<”或“=”)
①当![]() ,
,![]() 时,
时,![]() _____
_____![]() ;
;
②当![]() ,
,![]() 时,
时,![]() _____
_____![]() ;
;
③当![]() ,
,![]() 时,
时,![]() ______
______![]() ;
;
④当![]() ,
,![]() 时,
时,![]() ______
______![]() ;
;
⑤当![]() ,
,![]() 时,
时,![]() ______
______![]() ;
;
⑥当![]() ,
,![]() 时,
时,![]() _______
_______![]() ;
;
…
(2)归纳猜想:猜想并写出关于![]() 与
与![]() (
(![]() ,
,![]() 是常数,且
是常数,且![]() ,
,![]() )之间的数量关系;
)之间的数量关系;
(3)探究证明:请补全以下证明过程:
证明:根据一个实数的平方是非负数,可得![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
…
(4)实践应用:要制作面积为![]() 的长方形(或正方形)框架,直接利用探究得出的结论,求出框架周长的最小值.
的长方形(或正方形)框架,直接利用探究得出的结论,求出框架周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果mx+n=0,其中m、n为有理数,x为无理数,那么m=0且n=0.
(1)如果![]() ,其中a、b为有理数,那么a= ,b= .
,其中a、b为有理数,那么a= ,b= .
(2)如果![]() ,其中a、b为有理数,求a+2b的值.
,其中a、b为有理数,求a+2b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,给出下列结论:①b2=4ac,②abc<0;③a>c;④4a﹣2b+c<0,其中正确的个数有( )
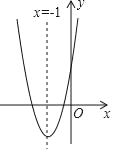
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
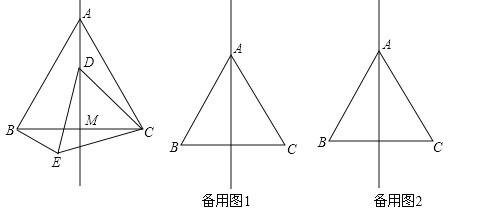
【题目】如图,在等边△ABC中,线段AM为BC边上的中线.动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.
(1)求∠CAM的度数;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
(3)当动D在直线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我区浙江中国花木城组织10辆汽车装运完A、B、C三种不同品质的苗木共100吨到外地销售,按计划10辆汽车都要装满,且每辆汽车只能装同一种苗木,由信息解答以下问题:
苗 木 品 种 | A | B | C |
每辆汽车运载量(吨) | 12 | 10 | 8 |
每吨苗木获利(万元) | 3 | 4 | 2 |
(1)设装A种苗木车辆数为x,装运B种苗木的车辆数为y,求y与x之间的函数关系式;
(2)若装运每种苗木的车辆都不少于2辆,则车辆安排方案有几种?写出每种安排方案
(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,P均在⊙O上,且分布在直径AB的两侧,BE⊥CP于点E.
(1)求证:△CAB∽△EPB;
(2)若AB=10,AC=6,BP=5,求CP的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com