
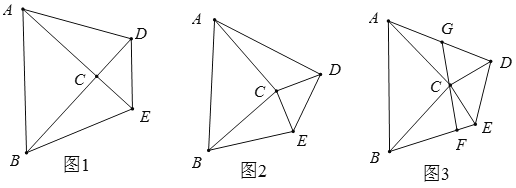
【题目】我们知道,如果两个三角形全等,则它们面积相等,而两个不全等的三角形,在某些情况下,可通过证明等底等高来说明它们的面积相等,已知![]() 与
与![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,连接
,连接![]() 、
、![]() .
.
(1)如图1,当![]() 时,求证
时,求证![]()
(2)如图2,当![]() 时,上述结论是否仍然成立?如果成立,请证明;如果不成立,说明理由.
时,上述结论是否仍然成立?如果成立,请证明;如果不成立,说明理由.
(3)如图3,在(2)的基础上,如果![]() 点为
点为![]() 的中点,连接
的中点,连接![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,试猜想
,试猜想![]() 与
与![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
【答案】(1)证明见解析;(2)成立,理由见解析;(3) GF⊥BE,证明见解析
【解析】
(1)由△ABC和△DEC是等腰直角三角形,即可得出相应的线段相等,从而可以证明出![]() ;
;
(2)作AG垂直于DC的延长线于G,作BH垂直于CE,垂足为H,利用题目已知条件可证的△ACG≌△BCH,从而知道AG=BH,即可得出![]() ;
;
(3) 延长CG到点H,连接AH,根据题目已知可证的△AGH≌△DGC,得到CD=AH,∠AHG=∠HCD,进一步证的△AHC≌△ECB,得到∠CEB=∠AHC=∠HCD,最后利用互余即可证得GF⊥BE.
证明:(1)∵△ABC和△DEC是等腰直角三角形
∴AC=CB,DC=CE,∠ACB=∠DCE=90°
∵∠BCE=90°
∴∠ACD=90°
∵![]() ,
,![]()
∴![]()
(2)成立
如图所示,作AG垂直于DC的延长线于G,作BH垂直于CE,垂足为H

∵∠DCE=90°
∴∠GCE=90°
∵BH⊥CE
∴∠BHC=90°
∴GD∥BH
∴∠GCB=∠CBH
∵∠GCB+∠ACG=90°,∠BCH+∠CBH=90°
∴∠BCH=∠ACG
在△ACG和△BCH中

∴△ACG≌△BCH
∴AG=BH
∵![]() ,
,![]() ,CE=CD
,CE=CD
∴![]()
(3)GF⊥BE

如图所示,延长CG到点H,使得HG=GC,连接AH
∵点G为AD的中点
∴AG=GD
在△AGH和△DGC

∴△AGH≌△DGC
∴CD=AH,∠AHG=∠HCD
∴AH∥CD
∴∠HAC+∠ACD=180°
∵∠ACB=∠DCE=90°
∴∠ACD+∠BCE=180°
∴∠HAC=∠BCE
∵△DCE是等腰三角形
∴CD=CE
∴CE=AH
在△AHC和△ECB中

∴△AHC≌△ECB
∴∠CEB=∠AHC=∠HCD
∵∠HCD+∠FCE=90°
∴∠FCE+∠CEF=90°
∴∠CFE=90°
∴GF⊥BE


科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,DE∥BC,点F在边AC上,DF与BE相交于点G,且∠EDF=∠ABE.

求证:(1)△DEF∽△BDE;(2)DGDF=DBEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:关于x的一元二次方程mx2﹣(2m﹣2)x+m=0有实根.
(1)求m的取值范围;
(2)若原方程两个实数根为x1,x2,是否存在实数m,使得![]() =1?请说明理由.
=1?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,直线y=2kx-2k (k>0)交y轴于点B,与直线y=kx交于点A.
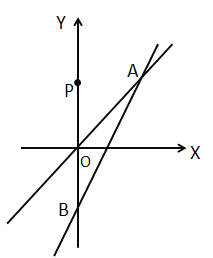
(1)求点A的横坐标;
(2)直接写出![]() 的x的取值范围;
的x的取值范围;
(3)若P(0,3)求PA+OA的最小值,并求此时k的值;
(4)若C(0,2)以A,B,C,D为顶点的四边形是以BC为一条边的菱形,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=﹣1,点B的坐标为(1,0),则下列结论:①AB=4;②b2﹣4ac>0;③ab<0;④a2﹣ab+ac<0,其中正确的结论有( )个.
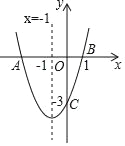
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:
(1)计算判断:(计算并判断大小,填写符号:“>”“<”或“=”)
①当![]() ,
,![]() 时,
时,![]() _____
_____![]() ;
;
②当![]() ,
,![]() 时,
时,![]() _____
_____![]() ;
;
③当![]() ,
,![]() 时,
时,![]() ______
______![]() ;
;
④当![]() ,
,![]() 时,
时,![]() ______
______![]() ;
;
⑤当![]() ,
,![]() 时,
时,![]() ______
______![]() ;
;
⑥当![]() ,
,![]() 时,
时,![]() _______
_______![]() ;
;
…
(2)归纳猜想:猜想并写出关于![]() 与
与![]() (
(![]() ,
,![]() 是常数,且
是常数,且![]() ,
,![]() )之间的数量关系;
)之间的数量关系;
(3)探究证明:请补全以下证明过程:
证明:根据一个实数的平方是非负数,可得![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
…
(4)实践应用:要制作面积为![]() 的长方形(或正方形)框架,直接利用探究得出的结论,求出框架周长的最小值.
的长方形(或正方形)框架,直接利用探究得出的结论,求出框架周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
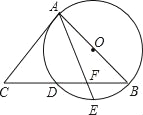
【题目】如图,AB是⊙O的直径,BC交⊙O于点D,E是![]() 的中点,AE与BC交于点F,∠C=2∠EAB.
的中点,AE与BC交于点F,∠C=2∠EAB.
(1)求证:AC是⊙O的切线;
(2)已知CD=4,CA=6,
①求CB的长;
②求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,给出下列结论:①b2=4ac,②abc<0;③a>c;④4a﹣2b+c<0,其中正确的个数有( )
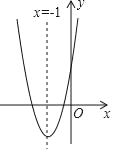
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com