
【题目】如图1,AB=AC=2,AD、BE为△ABC的两条高,F为AD上一点,且BD=DF,连接BF.
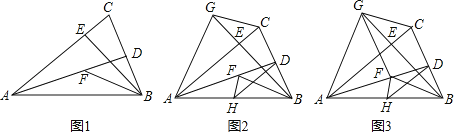
(1)求证:BF平分∠ABE;
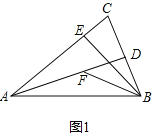
(2)如图2,延长BE至G点,使BG=AB,连结GC,取AB的中点H,连结FH、DH.
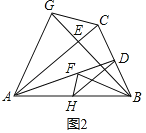
求证:①△DFH∽△BCG;②若BF=CG,BF∥CG,连结GF,如图3,求AD的长.
【答案】(1)证明见解析;(2)①证明见解析;②![]() .
.
【解析】
(1)首先证明∠CBE=∠CAD=∠BAD,再证明∠ABF+∠BAD=∠EBF+∠CBE=45°即可解决问题.
(2)①根据两边对应成比例夹角相等的两个三角形相似即可证明.
②如图3中,连接CF交BG于O.证明四边形BFGC是平行四边形,△BFC是等腰直角三角形即可解决问题.
(1)如图1中,
∵AD、BE为△ABC的两条高,
∴∠ADC=∠BEC=∠ADB=90°,
∴∠C+∠CAD=90°,∠C+∠CBE=90°,
∴∠CAD=∠CBE,
∵AC=AB,AD⊥BC,
∴∠CAD=∠BAD,
∴∠BAD=∠CBE,
∵DB=DE,∠BDF=90°,
∴∠DFB=∠DBF=45°,
∵∠DFB=∠FAB+∠FBA,∠DBF=∠CBE+∠EBF,
∴∠FAB+∠FBA=∠CBE+∠EBF,
∴∠ABF=∠EBF,
∴BF平分∠ABE;
(2)①如图2中,
∵∠ADB=90°,AH=HB,
∴DH=AH=BH,
∴∠HAD=∠HDA,
∵∠BAD=∠CBE,
∴∠ADH=∠CBG,
∵![]() ,
,![]() =
=![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
②如图3中,连接CF交BG于O.
∵BF=CG,BF∥CG,
∴四边形BFGC是平行四边形,
∴OF=OC,OB=OG=1,
∵FD垂直平分线段BC,
∴FC=FB,
∵∠FBD=45°,
∴△BFC是等腰直角三角形,
∴BF=2OF,
∵OB=1,
![]() ,即
,即![]()
解得:![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,
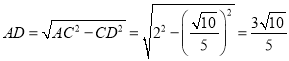 .
.


科目:初中数学 来源: 题型:
【题目】请用学过的方法研究一类新函数![]() (
(![]() 为常数,
为常数,![]() )的图象和性质.
)的图象和性质.
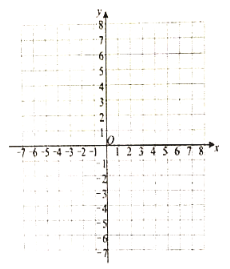
(1)在给出的平面直角坐标系中画出函数![]() 的图象;
的图象;
(2)对于函数![]() ,当自变量
,当自变量![]() 的值增大时,函数值
的值增大时,函数值![]() 怎样变化?
怎样变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
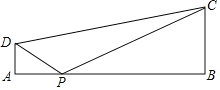
【题目】如图,在四边形ABCD中,∠A=∠B=90°,AB=6,AD=1,BC=2,P为AB边上的动点,当△PAD与△PBC相似时,PA=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知,抛物线![]() (a
(a![]() 0)的顶点为A(s,t)(其中s
0)的顶点为A(s,t)(其中s![]() 0) .
0) .
(1)若抛物线经过(2,2)和(-3,37)两点,且s=3.
①求抛物线的解析式;
②若n>3, 设点M(![]() ),N(
),N(![]() )在抛物线上,比较
)在抛物线上,比较![]() ,
,![]() 的大小关系,并说明理由;
的大小关系,并说明理由;
(2)若a=2,c=-2,直线![]() 与抛物线
与抛物线![]() 的交于点P和点Q,点P的横坐标为h,点Q的横坐标为h+3,求出b和h的函数关系式;
的交于点P和点Q,点P的横坐标为h,点Q的横坐标为h+3,求出b和h的函数关系式;
(3)若点A在抛物线![]() 上,且2≤s<3时,求a的取值范围.
上,且2≤s<3时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
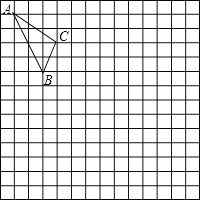
【题目】在如图的正方形网格中,每一个小正方形的边长为1格点△ABC(顶点是网格线交点的三角形)
(1)将△ABC向下平移6个单位得到△A1B1C1,画出△A1B1C1:
(2)将△A1B1C1绕点B顺时针旋转90°得到△A2B1C2画出△A2B1C2;
(3)求在平移和旋转变换过程中线段BC所扫过的图形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB为⊙O直径,弦CD⊥AB,垂足为H,点E为⊙O上一点,![]() ,BE与CD交于点F.
,BE与CD交于点F.
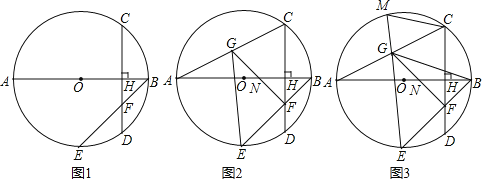
(1)如图1,求证:BH=FH;
(2)如图2,过点F作FG⊥BE,分别交AC、AB于点G、N,连接EG,求证:EB=EG;
(3)如图3,在(2)的条件下,延长EG交⊙O于M,连接CM、BG,若ON=1,△CMG的面积为6,求线段BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的进步和网络资源的丰富,在线学习已成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
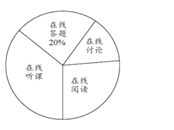
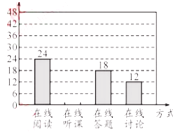
根据图中信息,解答下列问题:
(1)求本次调查的学生总人数,并补全条形统计图;
(2)求扇形统计图中“在线讨论”对应的扇形圆心角的度数;
(3)该校共有学生![]() 人,请你估计该校对在线阅读最感兴趣的学生人数.
人,请你估计该校对在线阅读最感兴趣的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() ,点
,点![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,![]() .
.
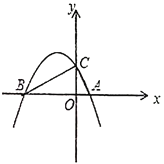
(1)求抛物线的解析式;
(2)点![]() 为抛物线第二象限上一点,满足
为抛物线第二象限上一点,满足![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)将直线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,与抛物线交于另一点
,与抛物线交于另一点![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校从甲、乙两名班主任中选拔一名参加教育局组织的班主任技能比赛,选拔内容分案例分析、班会设计、才艺展示三个项目,选拔比赛结束后,统计这两位班主任成绩并制成了如图所示的条形统计图:
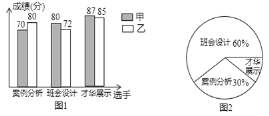
(1)乙班班主任三个项目的成绩中位数是 ;
(2)用6张相同的卡片分别写上甲、乙两名班主任的六项成绩,洗匀后,从中任意抽取一张,求抽到的卡片写有“80”的概率;
(3)若按照图12所示的权重比进行计算,选拔分数最高的一名班主任参加比赛,应确定哪名班主任获得参赛资格,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com