
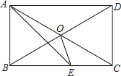
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() ________.
________.
【答案】![]()
【解析】
判断出△ABE是等腰直角三角形,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠ACB=30°,再判断出△ABO是等边三角形,根据等边三角形的性质求出OB=AB,再求出OB=BE,然后根据等腰三角形两底角相等求出∠BOE=75°,再根据∠AOE=∠AOB+∠BOE计算即可得解.
解:∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴∠AEB=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵∠CAE=15°,
∴∠ACE=∠AEB-∠CAE=45°-15°=30°,
∴∠BAO=90°-30°=60°,
∵矩形中OA=OB,
∴△ABO是等边三角形,
∴OB=AB,∠ABO=∠AOB=60°,
∴OB=BE,
∵∠OBE=∠ABC-∠ABO=90°-60°=30°,
∴∠BOE=![]() (180°-30°)=75°,
(180°-30°)=75°,
∴∠AOE=∠AOB+∠BOE,
=60°+75°,
=135°.
故答案为:135°.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
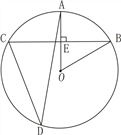
【题目】如图,在⊙O 中,BC是弦,OA⊥BC于点E,D为⊙O上一点,连接AD,CD.
(1)求证:∠AOB=2∠ADC;
(2)若OB⊥CD,CD=8,OE=![]() ,求tan∠ADC.
,求tan∠ADC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在菱形ABCD中,AB=2,∠BAD=60°,过点D作DE⊥AB点E,DF⊥BC于点F.将∠EDF绕点D顺时针旋转α°(0<α<180),其两边的对应边DE′、DF′分别与直线AB、BC相交于点G、P,如图2.连接GP,当△DGP的面积等于3![]() 时,则α的大小为( )
时,则α的大小为( )

A. 30 B. 45 C. 60 D. 120
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级同学参加社会实践活动,到“庐江台湾农民创业园”了解大棚蔬菜生长情况.他们分两组对西红柿的长势进行观察测量,分别收集到10株西红柿的高度,记录如下(单位:厘米)
第一组:32 39 45 55 60 54 60 28 56 41
第二组:51 56 44 46 40 53 37 47 50 46
根据以上数据,回答下列问题:
(1)第一组这10株西红柿高度的平均数是 ,中位数是 ,众数是 .
(2)小明同学计算出第一组方差为S12=122.2,请你计算第二组方差,并说明哪一组西红柿长势比较整齐.
查看答案和解析>>
科目:初中数学 来源: 题型:
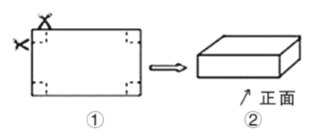
【题目】如图①是一张长为18![]() ,宽为12
,宽为12![]() 的长方形硬纸板,把它的四个角都剪去一个边长为
的长方形硬纸板,把它的四个角都剪去一个边长为![]() 的小正方形,然后把它折成一个无盖的长方体盒子(如图②),请回答下列问题:
的小正方形,然后把它折成一个无盖的长方体盒子(如图②),请回答下列问题:
(1)折成的无盖长方体盒子的容积![]()
![]() ;(用含
;(用含![]() 的代数式表示即可,不需化简)
的代数式表示即可,不需化简)
(2)请完成下表,并根据表格回答,当![]() 取什么正整数时,长方体盒子的容积最大?
取什么正整数时,长方体盒子的容积最大?
| 1 | 2 | 3 | 4 | 5 |
| 160 | ________ | 216 | ________ | 80 |
(3)从正面看折成的长方体盒子,它的形状可能是正方形吗?如果是正方形,求出![]() 的值;如果不是正方形,请说明理由.
的值;如果不是正方形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新华社消息:法国教育部宜布,小学和初中于2018年9月新学期开始,禁止学生在校使用手机.为了解学生手机使用情况,包河区某学校开展了“手机伴我健康行”的主题活动,学校随机抽取部分学生进行“使用手机的目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,图②的统计图.已知“查资料”的人数为40.

(1)本次抽样调查一共抽取了_________人;补全条形统计图;
(2)在扇形统计图中,“玩游戏”对应的圆心角的度数为_________度;
(3)该校共有学生2100人,请估计每周使用手机时间在2小时以上(不含2小时)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为改善生态环境,防止水土流失,某村计划在堤坡种植白杨树,现甲、乙两家林场有相同的白杨树苗可供选择,其具体销售方案如下:
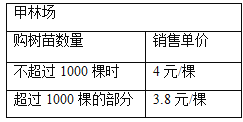
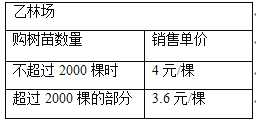
设购买白杨树苗x棵,到两家林场购买所需费用分别为![]() (元)、
(元)、![]() (元). 则:
(元). 则:
(1)该村需要购买1500棵白杨树苗,若都在甲林场购买所需费用为 元,若都在乙林场购买所需费用为 元;
(2)分别求出![]() 、
、![]() 与x之间的函数关系式;
与x之间的函数关系式;
(3)如果你是该村的负责人,应该选择到哪家林场购买树苗合算,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】云南鲁甸6.5级地震后,空军某部奉命赴灾区空投救灾物资,已知物资离开飞机在空中沿抛物线降落,抛物线的顶点在机舱舱口点A处(如图所示).
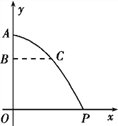
(1)若物体离开A处后下落的竖直高度AB=160 m时,水平距离BC=200 m,那么要使飞机在竖直高度OA=1 km的空中空投的物资恰好落在居民点P处,求飞机到点P处的水平距离OP应为多少;
(2)根据当时的风力测算,空投物资离开A处的竖直距离为160 m时,它到A处的水平距离将增至400 m.要使飞机在(1)中的点O正上方空投物资到P处,飞机离地面的高度应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD的对角线AC、BD相交于点O,AB=6,BC=8,若△AOB是等腰三角形,则平行四边形ABCD的面积等于_______________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com