
【题目】已知,如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)求证:2CD2=AD2+DB2.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)本题要判定△ACE≌△BCD,已知△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,则DC=EA,AC=BC,∠ACB=∠ECD,又因为两角有一个公共的角∠ACD,所以∠BCD=∠ACE,根据SAS得出△ACE≌△BCD.
(2)由(1)的论证结果得出∠DAE=90°,AE=DB,从而求出AD2+DB2=DE2,即2CD2=AD2+DB2.
证明:(1)∵△ABC和△ECD都是等腰直角三角形,
∴AC=BC,CD=CE,
∵∠ACB=∠DCE=90°,
∴∠ACE+∠ACD=∠BCD+∠ACD,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
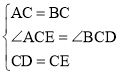 ,
,
∴△AEC≌△BDC(SAS);
(2)∵△ACB是等腰直角三角形,
∴∠B=∠BAC=45度.
∵△ACE≌△BCD,
∴∠B=∠CAE=45°
∴∠DAE=∠CAE+∠BAC=45°+45°=90°,
∴AD2+AE2=DE2.
由(1)知AE=DB,
∴AD2+DB2=DE2,即2CD2=AD2+DB2.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(3,0)、B(a,2)、C(0,m),D(n,0),且m2+n2=4,若E为CD中点.则AB+BE的最小值为( )
A. 3 B. 4 C. 5 D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
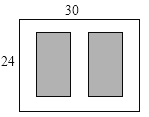
【题目】如图,某小区有一块长为30 m,宽为24 m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为480 m2,两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为________m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,先描出点![]() ,点
,点![]() .
.

(1)描出点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 的位置,写出
的位置,写出![]() 的坐标 ;
的坐标 ;
(2)用尺规在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小(保留作图痕迹);
的值最小(保留作图痕迹);
(3)用尺规在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() (保留作图痕迹).
(保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,点G是BC的中点,点H在AF上,动点P以每秒2cm的速度沿图1的边线运动,运动路径为:G→C→D→E→F→H,相应的△ABP的面积y(cm2)关于运动时间t(s)的函数图象如图2,若AB=6cm,则下列四个结论中正确的个数有( )①图1中的BC长是8cm,②图2中的M点表示第4秒时y的值为24cm2,③图1中的CD长是4cm,④图2中的N点表示第12秒时y的值为18cm2,⑤图1的总面积为72 cm2

A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,直线AB:y=﹣x+b交y轴于点A,交x轴于点B,S△AOB=8.

(1)求点B的坐标和直线AB的函数表达式;
(2)直线a垂直平分OB交AB于点D,交x轴于点E,点P是直线a上一动点,且在点D的上方,设点P的纵坐标为m.
①用含m的代数式表示△ABP的面积;
②当S△ABP=6时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青岛市某大酒店豪华间实行淡季、旺季两种价格标准,旺季每间比淡季上涨![]() ,下表是去年该酒店豪华间某两天的相关记录:
,下表是去年该酒店豪华间某两天的相关记录:
旺季 | 淡季 | |
未入住房间数 | 10 | 0 |
日总收入(元) | 24 000 | 40 000 |
(1)该酒店豪华间有多少间?旺季每间价格为多少元
(2)今年旺季来临,豪华间的间数不变。经市场调查发现,如果豪华间仍旧实行去年旺季价格,那么每天都客满;如果价格继续上涨,那么每增加25元,每天未入住房间数增加1间。不考虑其他因素,该酒店将豪华间的价格上涨多少元时,豪华间的日总收入最高?最高日总收入是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ADB=23°,E是AD上一点.将矩形沿CE折叠,点D的对应点F恰好落在BC上,CE交BD于H,连接HF,则∠BHF=__.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com