练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，矩形ABCD中，∠ADB=23°，E是AD上一点．将矩形沿CE折叠，点D的对应点F恰好落在BC上，CE交BD于H，连接HF，则∠BHF=__．

    【答案】44°

    【解析】

    由折叠可得∠CFH=∠CDH=67°，由平行线的性质可得∠DBC=∠ADB=23°，再根据∠CFH是△BFH的外角，即可得出∠BHF=∠CFH-∠CBD=44°．

    解：

    由题可得，∠CDH=∠CDE-∠HDE=90°-23°=67°，

    ∵矩形沿CE折叠，点D的对应点F恰好落在BC上，

    ∴∠CFH=∠CDH=67°，

    ∵AD∥BC，

    ∴∠DBC=∠ADB=23°，

    ∵∠CFH是△BFH的外角，

    ∴∠BHF=∠CFH-∠CBD=67°-23°=44°，

    故答案为：44°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知，如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点.

    （1）求证：△ACE≌△BCD；

    （2）求证：2CD2=AD2+DB2.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某水果超市为了吸引顾客来店购物，设立了一个如图所示的可以自由转动的转盘，开展有奖购物活动．顾客购买商品满200元就能获得一次转动转盘的机会，当转盘停止时，指针落在“一袋苹果”的区域就可以获得“一袋苹果”的奖品；指针落在“一盒樱桃”的区域就可以获得“一盒樱桃”的奖品．下表是该活动的一组统计数据：

    转动转盘的次数n

    100

    150

    200

    500

    800

    1000

    落在“一袋苹果”区域的次数m

    68

    108

    140

    355

    560

    690

    落在“一袋苹果”区域的频率

    0.68

    0.72

    0.70

    0.71

    0.70

    0.69

    下列说法不正确的是（　　）

    A. 当n很大时，估计指针落在“一袋苹果”区域的频率大约是0.70

    B. 假如你去转动转盘一次，获得“一袋苹果”的概率大约是0.70

    C. 如果转动转盘2000次，指针落在“一盒樱桃”区域的次数大约有600次

    D. 转动转盘10次，一定有3次获得“一盒樱桃”

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=4.41cm，BC=8.83cm，P是BC上一动点，连接AP，设P，C两点间的距离为xcm，P，A两点间的距离为ycm．（当点P与点C重合时，x的值为0）小东根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．下面是小东的探究过程，请补充完整：

    （1）通过取点、画图、测量，得到了x与y的几组值，如表：

    x/cm

    0

    0.43

    1.00

    1.50

    1.85

    2.50

    3.60

    4.00

    4.30

    5.00

    5.50

    6.00

    6.62

    7.50

    8.00

    8.83

    y/cm

    7.65

    7.28

    6.80

    6.39

    6.11

    5.62

    4.87

    　　

    4.47

    4.15

    3.99

    3.87

    3.82

    3.92

    4.06

    4.41

    （说明：补全表格时相关数值保留一位小数）

    （2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；

    （3）结合画出的函数图象，解决问题：当PA=PC时，PC的长度约为　　cm．（结果保留一位小数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，A（m，0），B（0，n），以B点为直角顶点在第二象限作等腰直角△ABC，则C点的坐标为_____．（用字母m、n表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市为解决部分市民冬季集中取暖问题，需铺设一条长4000米的管道，为尽量减少施工对交通造成的影响，施工时“…”，设实际每天铺设管道x米，则可得方程＝20，根据此情景，题中用“…”表示的缺失的条件应补为（　　）

    A. 每天比原计划多铺设10米，结果延期20天完成

    B. 每天比原计划少铺设10米，结果延期20天完成

    C. 每天比原计划多铺设10米，结果提前20天完成

    D. 每天比原计划少铺设10米，结果提前20天完成

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，三个顶点的坐标分别为、、.

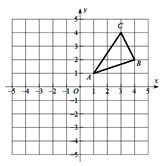
    (1)若与关于y轴成轴对称，则三个顶点坐标分别为_________，____________，____________；

    (2)若P为x轴上一点，则的最小值为____________；

    (3)计算的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地，乙车比甲车晚出发2小时（从甲车出发时开始计时），图中折线OABC、线段DE分别表示甲、乙两车所行路程y（千米）与时间x（小时）之间的函数关系对应的图像线段AB表示甲出发不足2小时因故停车检修），请根据图像所提供的信息，解决如下问题：

    （1）求乙车所行路程y与时间x的函数关系式；

    （2）求两车在途中第二次相遇时，它们距出发地的路程；

    （3）乙车出发多长时间，两车在途中第一次相遇？（写出解题过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场购进一种单价为元的商品，如果以单价元售出，那么每天可卖出个，根据销售经验，每降价元，每天可多卖出个，假设每个降价（元），每天销售（个），每天获得利润（元）．

    写出与的函数关系式________；

    求出与的函数关系式（不必写出的取值范围）

    查看答案和解析>>

    同步练习册答案