
【题目】如图,A(m,0),B(0,n),以B点为直角顶点在第二象限作等腰直角△ABC,则C点的坐标为_____.(用字母m、n表示)

【答案】(﹣n,n﹣m)
【解析】
过点C作CD⊥y轴于点D,由△ABC为等腰直角三角形即可得出∠ABC=90°、AB=BC,通过角的计算即可得出∠ABO=∠BCD,再结合∠CDB=∠BOA=90°即可利用AAS证出△ABO和△BCD,由此即可得出BD、CD的长度,进而可得出点C的坐标.
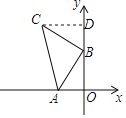
解:过点C作CD⊥y轴于点D,如图所示.
∵△ABC为等腰直角三角形,
∴∠ABC=90°,AB=BC.
∵CD⊥BD,BO⊥AO,
∴∠CDB=∠BOA=90°.
∵∠CBD+∠ABO=90°,∠CBD+∠BCD=90°,
∴∠ABO=∠BCD.
在△ABO和△BCD中,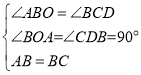 ,
,
∴△ABO≌△BCD(AAS),
∴BD=AO,CD=BO,
∵A(m,0),B(0,n),
∴BD=﹣m,CD=n,
∴点C的坐标为(﹣n,n﹣m),
故答案为:(﹣n,n﹣m).


科目:初中数学 来源: 题型:
【题目】已知:如图1,点G是BC的中点,点H在AF上,动点P以每秒2cm的速度沿图1的边线运动,运动路径为:G→C→D→E→F→H,相应的△ABP的面积y(cm2)关于运动时间t(s)的函数图象如图2,若AB=6cm,则下列四个结论中正确的个数有( )①图1中的BC长是8cm,②图2中的M点表示第4秒时y的值为24cm2,③图1中的CD长是4cm,④图2中的N点表示第12秒时y的值为18cm2,⑤图1的总面积为72 cm2

A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴负半轴交于点
轴负半轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() .
.
(1)求抛物线的解析式;
(2)点![]() 在
在![]() 轴上,且
轴上,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)点![]() 在抛物线上,点
在抛物线上,点![]() 在抛物线的对称轴上,是否存在以点
在抛物线的对称轴上,是否存在以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在。求出所有符合条件的点
为顶点的四边形是平行四边形?若存在。求出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“求作∠AOB的角平分线”的尺规作图过程.
已知:如图,钝角∠AOB.
求作:∠AOB的角平分线.
作法:
①在OA和OB上,分别截取OD、OE,使OD=OE;
②分别以D、E为圆心,大于![]() DE的长为半径作弧,在∠AOB内,两弧交于点C;
DE的长为半径作弧,在∠AOB内,两弧交于点C;
③作射线OC.
所以射线OC就是所求作的∠AOB的角平分线.
请回答:该尺规作图的依据是__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中,∠CAB=90°,F是AB边上一点,作射线CF,过点B作BG⊥CF于点G,连接AG.
(1)求证:∠ABG=∠ACF;
(2)用等式表示线段CG,AG,BG之间的等量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ADB=23°,E是AD上一点.将矩形沿CE折叠,点D的对应点F恰好落在BC上,CE交BD于H,连接HF,则∠BHF=__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区决定购置一批共享单车,经市场调查得知,购买3辆男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需1600元.
(1)求男式单车和女式单车每辆分别是多少元?
(2)该社区要求男式单车比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过5000元,问该社区有几种购置方案?怎样的购置才能使所需总费用最低?最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买一批篮球和足球,已知购买2个篮球和1个足球共需320元,购买3个篮球和2个足球共需540元.
(1)求每个篮球和每个足球的售价;
(2)如果学校计划购买这两种球共50个,总费用不超过5500元,那么最多可购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于抛物线![]() .
.
![]() 它与
它与![]() 轴交点的坐标为________,与
轴交点的坐标为________,与![]() 轴交点的坐标为________,顶点坐标为________.
轴交点的坐标为________,顶点坐标为________.
![]() 在所给的平面直角坐标系中画出此时抛物线;
在所给的平面直角坐标系中画出此时抛物线;
![]() 结合图象回答问题:当
结合图象回答问题:当![]() 时,
时,![]() 的取值范围是________.
的取值范围是________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com