
【题目】如图,在等腰直角△ABC中,∠CAB=90°,F是AB边上一点,作射线CF,过点B作BG⊥CF于点G,连接AG.
(1)求证:∠ABG=∠ACF;
(2)用等式表示线段CG,AG,BG之间的等量关系,并证明.

【答案】(1)证明见解析;(2)CG=![]() AG+BG,证明见解析.
AG+BG,证明见解析.
【解析】
(1)根据等腰直角三角形的性质解答即可;
(2)在CG上截取CH=BG,连接AH,利用全等三角形的判定和性质解答即可.
(1)证明:
∵∠CAB=90°.
∵BG⊥CF于点G,
∴∠BGF=∠CAB=90°.
∵∠GFB=∠CFA
∴∠ABG=∠ACF
(2)CG=![]() AG+BG
AG+BG
在CG上截取CH=BG,连接AH,
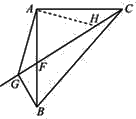
∵△ABC是等腰直角三角形,
∴∠CAB=90°,AB=AC.
∵∠ABG=∠ACH.
∴△ABG≌△ACH,
∴AG=AH,∠GAB=∠HAC.
∴∠GAH=90°.
∴AG2+AH2=GH2.
∴GH=![]() AG,
AG,
∴CG=CH+GH=![]() AG+BG,
AG+BG,


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点E为边AB上任意一点,点D在边CB的延长线上,且ED=EC.

(1)当点E为AB的中点时(如图1),则有AE DB(填“>”“<”或“=”);
(2)猜想AE与DB的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境:在数学活动课上,老师出示了这样一个问题:如图1,在矩形ABCD中,AD=2AB,E是AB延长线上一点,且BE=AB,连接DE,交BC于点M,以DE为一边在DE的左下方作正方形DEFG,连接AM.试判断线段AM与DE的位置关系.
探究展示:勤奋小组发现,AM垂直平分DE,并展示了如下的证明方法:
证明:∵BE=AB,∴AE=2AB.
∵AD=2AB,∴AD=AE.
∵四边形ABCD是矩形,∴AD∥BC.
∴![]() .(依据1)
.(依据1)
∵BE=AB,∴![]() .∴EM=DM.
.∴EM=DM.
即AM是△ADE的DE边上的中线,
又∵AD=AE,∴AM⊥DE.(依据2)
∴AM垂直平分DE.
反思交流:
(1)①上述证明过程中的“依据1”“依据2”分别是指什么?
②试判断图1中的点A是否在线段GF的垂直平分线上,请直接回答,不必证明;
(2)创新小组受到勤奋小组的启发,继续进行探究,如图2,连接CE,以CE为一边在CE的左下方作正方形CEFG,发现点G在线段BC的垂直平分线上,请你给出证明;
探索发现:
(3)如图3,连接CE,以CE为一边在CE的右上方作正方形CEFG,可以发现点C,点B都在线段AE的垂直平分线上,除此之外,请观察矩形ABCD和正方形CEFG的顶点与边,你还能发现哪个顶点在哪条边的垂直平分线上,请写出一个你发现的结论,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC为等边三角形,点D为直线BC上一动点(点D不与点B,点C重合).以AD为边作等边三角形ADE,连接CE.
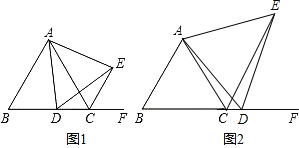
(1)如图1,当点D在边BC上时.求证:△ABD≌△ACE;
(2)如图2,当点D在边BC的延长线上时,其他条件不变,请写出BC,DC,CE之间存在的数量关系,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国汉代数学家赵爽为了证明勾股定理,创造了一幅“弦图”后人称其为“赵爽弦图”(如图1).图2是弦图变化得到,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=10,求S2的值.以下是求S2的值的解题过程,请你根据图形补充完整.
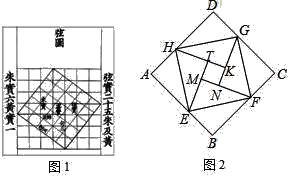
解:设每个直角三角形的面积为S
S1﹣S2= (用含S的代数式表示)①
S2﹣S3= (用含S的代数式表示)②
由①,②得,S1+S3= 因为S1+S2+S3=10,
所以2S2+S2=10.
所以S2=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() 中,
中,![]() ,D为BC的中点,过点C作
,D为BC的中点,过点C作![]() 于点G,过点B作
于点G,过点B作![]() 于点B,交CG的延长线于点F,连接DF交AB于点E.
于点B,交CG的延长线于点F,连接DF交AB于点E.
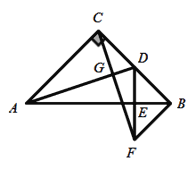
(1)求证:![]() ;
;
(2)求证:AB垂直平分DF;
(3)连接AF,试判断![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某加工厂投资兴建2条全自动生产线和1条半自动生产线共需资金26万元,而投资兴建1条全自动生产线和3条半自动生产线共需资金28万元
(1)求每条全自动生产线和半自动生产线的成本各为多少万元?
(2)据预测,2015年每条全自动生产线的毛利润为26万元,每条半自动生产线的毛利润为16万元.这-年,该加工厂共投资兴建10条生产线,若想获得不少于120万元的纯利润,则2015年该加工厂至少需投资兴建多少条全自动生产线?(纯利润=毛利润-成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com