Question

【题目】如图，在等腰中，，D为BC的中点，过点C作于点G，过点B作于点B，交CG的延长线于点F，连接DF交AB于点E.

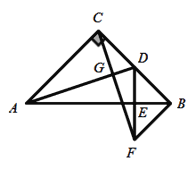
(1)求证：；

(2)求证：AB垂直平分DF；

(3)连接AF，试判断的形状，并说明理由.

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）△ACF是等腰三角形，理由见解析.

【解析】

（1）先由CG⊥AD得到∠AGC=90°，证得∠CAD=∠FCB，再由AC=BC，FB⊥BC，根据“ASA”即可得出结论；

（2）由（1）△ACD≌△CBF，得出CD=BF，证得BD=BF，由△ABC是等腰直角三角形，得出∠DBE=45°，再证得∠DBE=∠FBE=45°，由“SAS”证出△DBE≌△FBE即可得出结论；

（3）由△CBF≌△ACD，得出CF=AD，由AB垂直平分DF，得出AF=AD，证得CF=AF，即可得出结论．

证明：（1）∵CG⊥AD，

∴∠AGC=90°，

∴∠GCA+∠CAD=90°，

∵∠GCA+∠FCB=90°，

∴∠CAD=∠FCB，

∵FB⊥BC，

∴∠CBF=90°，

∵Rt△ABC是等腰三角形，∠ACB=90°，

∴AC=BC，∠CBF=∠ACB，

在△ACD和△CBF中

，

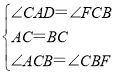∴△ACD≌△CBF（ASA）；

（2）∵△ACD≌△CBF，

∴CD=BF，

∵D为BC的中点，

∴CD=BD，

∴BD=BF，

∵△ABC是等腰直角三角形，∠ACB=90°，

∴∠DBE=45°，

∵∠CBF=90°，

∴∠DBE=∠FBE=45°，

在△DBE和△FBE中

，

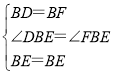∴△DBE≌△FBE（SAS），

∴DE=FE，∠DEB=∠FEB=90°，

∴AB垂直平分DF；

（3）△ACF是等腰三角形，理由为：

连接AF，如图所示，

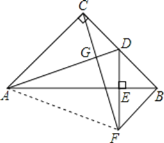
由（1）知：△CBF≌△ACD，

∴CF=AD，

由（2）知：AB垂直平分DF，

∴AF=AD，

∵CF=AD，

∴CF=AF，

∴△ACF是等腰三角形．