
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
![]() 若
若![]() 是这个方程的一个根,求
是这个方程的一个根,求![]() 的值和方程的另一个根;
的值和方程的另一个根;
![]() 求证:对于任意实数
求证:对于任意实数![]() ,这个方程都有两个不相等的实数根.
,这个方程都有两个不相等的实数根.
【答案】(1)当![]() 时,原方程为
时,原方程为![]() ,则方程的另一个根为
,则方程的另一个根为![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)把x=2代入方程得出关于m的方程,求出m的值再代入原方程求出x的另一个根.
(2)只要证明△>0,即可得出方程有两不相等的实数根.
(1)把x=﹣2代入方程,得:4﹣2(m﹣1)(﹣2)﹣m(m+2)=0.
即m2﹣2m=0.
解得:m1=0,m2=2.
当m=0时,原方程为x2+2x=0.
则方程的另一个根为x=0.
当m=2时,原方程为x2﹣2x﹣8=0,则方程的另一个根为x=4.
(2)△=[﹣2(m﹣1)]2﹣4×[﹣m(m+2)]=8m2+4.
∵对于任意实数m,m2≥0,∴8m2+4>0,∴对于任意实数m,这个方程都有两个不相等的实数根.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC为等边三角形,点D为直线BC上一动点(点D不与点B,点C重合).以AD为边作等边三角形ADE,连接CE.
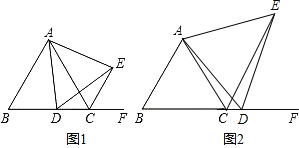
(1)如图1,当点D在边BC上时.求证:△ABD≌△ACE;
(2)如图2,当点D在边BC的延长线上时,其他条件不变,请写出BC,DC,CE之间存在的数量关系,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() 中,
中,![]() ,D为BC的中点,过点C作
,D为BC的中点,过点C作![]() 于点G,过点B作
于点G,过点B作![]() 于点B,交CG的延长线于点F,连接DF交AB于点E.
于点B,交CG的延长线于点F,连接DF交AB于点E.
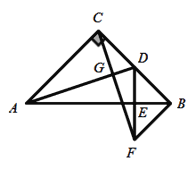
(1)求证:![]() ;
;
(2)求证:AB垂直平分DF;
(3)连接AF,试判断![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 为线段
为线段![]() 上一动点,以每秒
上一动点,以每秒![]() 的速度从
的速度从![]() 匀速运动到
匀速运动到![]() ,过
,过![]() 作直线
作直线![]() ,且
,且![]() ,点
,点![]() 在直线
在直线![]() 的右侧,设点
的右侧,设点![]() 运动时间为
运动时间为![]() .
.
(1)当![]() 为等腰三角形时,
为等腰三角形时,![]() ;
;
(2)当![]() 点在线段
点在线段![]() 上时,过
上时,过![]() 点作
点作![]() 于点
于点![]() ,求证
,求证![]() ;
;
(3)当![]() 点在线段
点在线段![]() 上运动的过程中,
上运动的过程中,![]() 的面积是否变化?若不变,求出它的值.
的面积是否变化?若不变,求出它的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
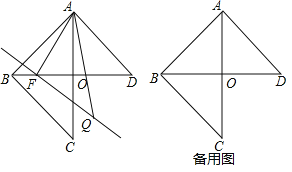
【题目】如图:![]() 中,
中,![]() .
.

![]() 求作
求作![]() 边上的垂直平分线
边上的垂直平分线![]() ,使得
,使得![]() 交
交![]() 于
于![]() ;将线段
;将线段![]() 沿着
沿着![]() 的方向平移到线段
的方向平移到线段![]() (其中点
(其中点![]() 平移到点
平移到点![]() ,画出平移后的线段
,画出平移后的线段![]() ;(要求用尺规作图,不写作法,保留作图痕迹.)
;(要求用尺规作图,不写作法,保留作图痕迹.)
![]() 连接
连接![]() 、
、![]() ,试判断四边形
,试判断四边形![]() 是矩形吗?说明理由.
是矩形吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某加工厂投资兴建2条全自动生产线和1条半自动生产线共需资金26万元,而投资兴建1条全自动生产线和3条半自动生产线共需资金28万元
(1)求每条全自动生产线和半自动生产线的成本各为多少万元?
(2)据预测,2015年每条全自动生产线的毛利润为26万元,每条半自动生产线的毛利润为16万元.这-年,该加工厂共投资兴建10条生产线,若想获得不少于120万元的纯利润,则2015年该加工厂至少需投资兴建多少条全自动生产线?(纯利润=毛利润-成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
销售单价(元) | x |
销售量y(件) |
|
销售玩具获得利润w(元) |
|
(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国家的宏观调控下,某市的商品房成交价由今年3月份的5000元/m2下降到5月份的4050元/m2.
(1)问4、5两月平均每月降价的百分率是多少?
(2)如果房价继续回落,按此降价的百分率,你预测到7月分该市的商品房成交均价是否会跌破3000元/m2?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com