
【题目】已知△ABC为等边三角形,点D为直线BC上一动点(点D不与点B,点C重合).以AD为边作等边三角形ADE,连接CE.
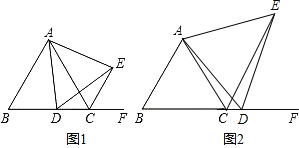
(1)如图1,当点D在边BC上时.求证:△ABD≌△ACE;
(2)如图2,当点D在边BC的延长线上时,其他条件不变,请写出BC,DC,CE之间存在的数量关系,并写出证明过程.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据等边三角形的性质就可以得出∠BAC=∠DAE=60°,AB=BC=AC,AD=DE=AE,进而就可以得出△ABD≌△ACE;
(2)由等边三角形的性质就可以得出∠BAC=∠DAE=60°,AB=BC=AC,AD=DE=AE,进而就可以得出△ABD≌△ACE,就可以得出BC+CD=CE.
(1)∵△ABC和△ADE是等边三角形,
∴∠BAC=∠DAE=60°,AB=BC=AC,AD=DE=AE.
∴∠BAC∠DAC=∠DAE∠DAC,
∴∠BAD=∠EAC.
在△ABD和△ACE中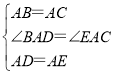 ,
,
∴△ABD≌△ACE(SAS).
(2)BC+CD=CE.
∵△ABC和△ADE是等边三角形,
∴∠BAC=∠DAE=60°,AB=BC=AC,AD=DE=AE.
∴∠BAC+∠DAC=∠DAE+∠DAC,
∴∠BAD=∠EAC.
在△ABD和△ACE中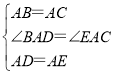 ,
,
∴△ABD≌△ACE(SAS).
∴BD=CE.
∵BD=BC+CD,
∴CE=BC+CD;


科目:初中数学 来源: 题型:
【题目】已知函数y=(2m+1)x+m﹣3.
(1)若函数图象经过原点,求m的值;
(2)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围;
(3)若这个函数是一次函数,且图象不经过第四象限,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴负半轴交于点
轴负半轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() .
.
(1)求抛物线的解析式;
(2)点![]() 在
在![]() 轴上,且
轴上,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)点![]() 在抛物线上,点
在抛物线上,点![]() 在抛物线的对称轴上,是否存在以点
在抛物线的对称轴上,是否存在以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在。求出所有符合条件的点
为顶点的四边形是平行四边形?若存在。求出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在∠MON的角平分线上,过点P作OP的垂线交OM,ON于C、D,PA⊥OM.PB⊥ON,垂足分别为A、B,EP∥BD,则下列结论错误的是( )
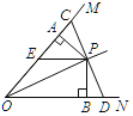
A.CP=PDB.PA=PBC.PE=OED.OB=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“求作∠AOB的角平分线”的尺规作图过程.
已知:如图,钝角∠AOB.
求作:∠AOB的角平分线.
作法:
①在OA和OB上,分别截取OD、OE,使OD=OE;
②分别以D、E为圆心,大于![]() DE的长为半径作弧,在∠AOB内,两弧交于点C;
DE的长为半径作弧,在∠AOB内,两弧交于点C;
③作射线OC.
所以射线OC就是所求作的∠AOB的角平分线.
请回答:该尺规作图的依据是__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中,∠CAB=90°,F是AB边上一点,作射线CF,过点B作BG⊥CF于点G,连接AG.
(1)求证:∠ABG=∠ACF;
(2)用等式表示线段CG,AG,BG之间的等量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区决定购置一批共享单车,经市场调查得知,购买3辆男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需1600元.
(1)求男式单车和女式单车每辆分别是多少元?
(2)该社区要求男式单车比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过5000元,问该社区有几种购置方案?怎样的购置才能使所需总费用最低?最低费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com