
【题目】在平面直角坐标系中,A(3,0)、B(a,2)、C(0,m),D(n,0),且m2+n2=4,若E为CD中点.则AB+BE的最小值为( )
A. 3 B. 4 C. 5 D. 2![]()
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】小丽和小华想利用摸球游戏决定谁去参加市里举办的书法比赛,游戏规则是:在一个不透明的袋子里装有除数字外完全相同的4个小球,上面分别标有数字2,3,4,5.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为偶数,则小丽去参赛;否则小华去参赛.
(1)用列表法或画树状图法,求小丽参赛的概率.
(2)你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
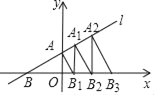
【题目】如图,在平面直角坐标系中,直线l:y=![]() x+1交x轴于点B,交y轴于点A,过点A作AB1⊥AB交x轴于点B1,过点B1作B1A1⊥x轴交直线l于点A2…依次作下去,则点Bn的横坐标为_____.
x+1交x轴于点B,交y轴于点A,过点A作AB1⊥AB交x轴于点B1,过点B1作B1A1⊥x轴交直线l于点A2…依次作下去,则点Bn的横坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
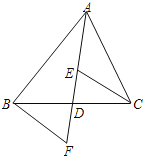
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE.下列说法:①△BDF≌△CDE;②CE=BF; ③BF∥CE;④△ABD和△ACD周长相等.其中正确的有___________(只填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有10个数据x1,x2,…x10,已知它们的和为2018,当代数式(x﹣x1)2+(x﹣x2)2+…+(x﹣x10)2取得最小值时,x的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣9ax+18a的图象与x轴交于A,B两点(A在B的左侧),图象的顶点为C,直线AC交y轴于点D.
(1)连接BD,若∠BDO=∠CAB,求这个二次函数的表达式;
(2)是否存在以原点O为对称轴的矩形CDEF?若存在,求出这个二次函数的表达式,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() :
:![]() 与直线
与直线![]() :
:![]() 交于点
交于点![]() ,则
,则![]() ______.
______.

【答案】-1
【解析】
将点A的坐标代入两直线解析式得出关于m和b的方程组,解之可得.
解:由题意知![]() ,
,
解得![]() ,
,
故答案为:![]() .
.
【点睛】
本题主要考查两直线相交或平行问题,解题的关键是掌握两直线的交点坐标必定同时满足两个直线解析式.
【题型】填空题
【结束】
11
【题目】如图,长方形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则△AFC的面积等于___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)求证:2CD2=AD2+DB2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com