
����Ŀ�����壺���һ��ֱ����һ����������ֻ��һ�����㣬������λ��ֱ�ߵ�ͬ�ԣ���֮Ϊֱ�����������У�����ֱ�߽������ߵ����ߣ�ֱ�������ߵ�Ψһ��������е㣮
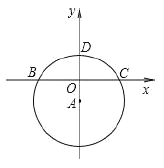
��1����ͼ����ƽ��ֱ������ϵ�У���![]() Ϊ����ԭ�㣬�Ե�
Ϊ����ԭ�㣬�Ե�![]() ΪԲ�ģ�5Ϊ�뾶��Բ
ΪԲ�ģ�5Ϊ�뾶��Բ![]() ����
����![]() ��ĸ������ڵ�
��ĸ������ڵ�![]() �������
�������![]() ��Բ
��Բ![]() �����ߵĽ���ʽ��
�����ߵĽ���ʽ��
��2����������![]() ��
��![]() ����ֱ��
����ֱ��![]() ��
��![]() �������ڵ�
�������ڵ�![]() ����ֱ�ߵĽ���ʽ��
����ֱ�ߵĽ���ʽ��
��3��������![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() ���У��ҵ�
���У��ҵ�![]() ʱ��
ʱ��![]() ����СֵΪ
����СֵΪ![]() ����
����![]() ��ֵ��
��ֵ��
���𰸡���1��![]() ����2��
����2��![]() ����3��1��
����3��1��![]()
��������
��1������![]() ����
����![]() ��
��![]() ����
����![]() ����
����![]() ����Ϊ
����Ϊ![]() ����
����![]() ��
��![]() ���ߣ�����
���ߣ�����![]() ���ټӹ�����
���ټӹ�����![]() ����֤
����֤![]() ���ɶ�Ӧ�߳ɱ�������
���ɶ�Ӧ�߳ɱ�������![]() �ij��������õ�
�ij��������õ�![]() ���꣬������ֱ��
���꣬������ֱ��![]() ����ʽ��
����ʽ��
��2���ֱ�ѵ�![]() ���������ߺ�ֱ�߽���ʽ����������߽���ʽΪ
���������ߺ�ֱ�߽���ʽ����������߽���ʽΪ![]() ��ֱ�߽���ʽ����ȥ
��ֱ�߽���ʽ����ȥ![]() ��
��![]() ������ֱ�������������У�ֻ��һ�����㣩������������ʽ�õ�����
������ֱ�������������У�ֻ��һ�����㣩������������ʽ�õ�����![]() �ķ�����������ȵ�ʵ����������
�ķ�����������ȵ�ʵ����������![]() �������
�������![]() ��ֵ��
��ֵ��
��3����Ϊ���κ���ͼ����ֱ�����У����Ѷ��κ�����ֱ�߽���ʽ�������õ�����![]() �ķ��������������ʵ����������
�ķ��������������ʵ����������![]() ��������ʽ��
��������ʽ��![]() ���ɿ���
���ɿ���![]() ����
����![]() �Ķ��κ�������Ӧ�����߿������ϣ��Գ���Ϊֱ��
�Ķ��κ�������Ӧ�����߿������ϣ��Գ���Ϊֱ��![]() ���������۶Գ�����
���������۶Գ�����![]() ��ࡢ�м䡢�Ҳ��������������ͼ�εã������Գ�����
��ࡢ�м䡢�Ҳ��������������ͼ�εã������Գ�����![]() ��༴
��༴![]() ʱ����ͼ���֪
ʱ����ͼ���֪![]() ʱ
ʱ![]() ��
��![]() ���������������
���������������![]() ʱ
ʱ![]() ȡ����Сֵ����
ȡ����Сֵ����![]() ��
��![]() ����õ�����
����õ�����![]() �ķ��̣������⣻�����Գ�����
�ķ��̣������⣻�����Գ�����![]() ��Χ��ʱ��
��Χ��ʱ��![]() ʱ��ȡ����Сֵ
ʱ��ȡ����Сֵ![]() ���÷���
���÷���![]() ����ã�
����ã�![]() �������Գ�����2���Ҳ༴
�������Գ�����2���Ҳ༴![]() ʱ����ͼ���֪
ʱ����ͼ���֪![]() ʱ
ʱ![]() ��
��![]() ���������������
���������С������![]() ʱ
ʱ![]() ȡ����Сֵ����
ȡ����Сֵ����![]() ��
��![]() ���뼴���
���뼴���![]() ��ֵ��
��ֵ��
�⣺��1����ͼ1������![]() ���ǹ���
���ǹ���![]() ��
��![]() ���߽�
���߽�![]() ���ڵ�
���ڵ�![]()
![]() ��
��![]()
![]() ��
��![]()
![]()
![]()
![]()
![]() ��
��![]()
![]()
![]()
![]()
![]()
![]()
![]()
��ֱ��![]() ����ʽΪ��
����ʽΪ��![]()
![]() ����ã�
����ã�![]()
![]() ����
����![]() ��
��![]() �����ߵĽ���ʽΪ
�����ߵĽ���ʽΪ![]() ;
;
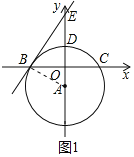
��2��![]() ������
������![]() ������
������![]()
![]() ����ã�
����ã�![]()
![]() �����߽���ʽ��
�����߽���ʽ��![]()
![]() ֱ��
ֱ��![]() ������
������![]()
![]() ���ɵã�
���ɵã�![]()
![]() ֱ�߽���ʽΪ��
ֱ�߽���ʽΪ��![]()
![]() ֱ��������������
ֱ��������������
![]() ����
����![]() �ķ���
�ķ���![]() ��������ȵ�ʵ����
��������ȵ�ʵ����
���������ã�![]()
![]() ��
��![]()
��ã�![]()
![]() ֱ�߽���ʽΪ
ֱ�߽���ʽΪ![]() ��
��
��3��![]() ����
����![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() ����
����
![]() ����
����![]() �ķ���
�ķ���![]() ��������ȵ�ʵ����
��������ȵ�ʵ����
���������ã�![]()
![]() ��
��![]()
�����ã�![]() ���ɿ���
���ɿ���![]() ����
����![]() �Ķ��κ�����
�Ķ��κ�����
��Ӧ�����߿������ϣ��Գ���Ϊֱ��![]()
![]() ��
��![]() ʱ��
ʱ��![]() ����СֵΪ
����СֵΪ![]()
����ͼ2����![]() ʱ����
ʱ����![]() ʱ
ʱ![]() ��
��![]() �����������
�����������
![]() ʱ��
ʱ��![]() ȡ����Сֵ
ȡ����Сֵ![]()
![]() �������⣻
�������⣻

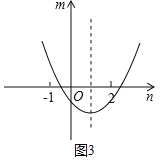
����ͼ3����![]() ʱ��
ʱ��![]() ʱ��
ʱ��![]() ȡ����Сֵ
ȡ����Сֵ![]()
![]() ����ã�
����ã�![]() ��
��
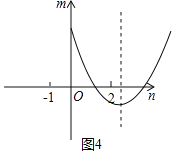
����ͼ4����![]() ʱ����
ʱ����![]() ʱ
ʱ![]() ��
��![]() ���������С
���������С
![]() ʱ��
ʱ��![]() ȡ����Сֵ
ȡ����Сֵ![]()
![]() ����ã�
����ã�![]() ��
��![]() ����ȥ��
����ȥ��
����������![]() ��ֵΪ1��
��ֵΪ1��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
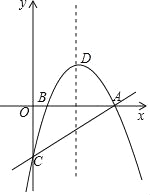
����Ŀ����ͼ��������y=ax2+bx+c��x�ύ��A��B��1��0�����㣬��y�ύ�ڵ�C��ֱ��y=![]() x��2����A��C���㣬�����ߵĶ���ΪD��
x��2����A��C���㣬�����ߵĶ���ΪD��
��1���������ߵĽ���ʽ������D�����ꣻ
��2����ֱ��AC�Ϸ����������ϴ���һ��P��ʹ��PAC����������ֱ��д��P�����꼰��PAC��������ֵ��
��3����y�����Ƿ����һ��G��ʹ��GD+GB��ֵ��С�������ڣ������G�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ϲ��غ�ij����վA���һ�ȴ��籩��A����ƫ��30���ķ���ӭ������վϮ������֪�÷籩�ٶ�ΪÿСʱ20ǧ�ף��籩��Χ50ǧ��Χ�ڽ��ܵ�Ӱ�죬���÷籩���ı��ٶ��뷽��������վ���Ϸ�60ǧ�״����غ�����B�Ƿ������η籩��Ӱ�죿������Ӱ�죬��˵�����ɣ�����Ӱ�죬�������Ӱ���ʱ�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������ֽ��ABC����ACB��90�㣬AC��3��AB��5����������ƽ��ֱ������ϵ�У���ͼ��ʾ��AC��y�ᣬBC��x�ᣬ����A��Bǡ�ö��ڷ���������y��![]() ��ͼ���ϣ�AC��BC���ӳ��߷ֱ�x�ᡢy����D��E���㣬���C������Ϊ(m��n)��
��ͼ���ϣ�AC��BC���ӳ��߷ֱ�x�ᡢy����D��E���㣬���C������Ϊ(m��n)��
(1)��A��B���������(��m��n������k)��
(2)��m��n��0.5ʱ����÷����������Ľ���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
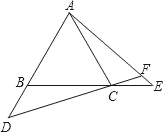
����Ŀ����ͼ����֪�ڵȱ�������ABC�У���D��E�ֱ���AB��BC�ӳ����ϵĵ㣬��BD��CE��ֱ��CD��AE�ཻ�ڵ�F��
��1����֤��DC��AE��
��2����֤��AD2��DCDF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��y��2x��m��������y��ax2��ax��b��һ��������M(1��0)����a��b.
(1)�������߶���Q�����꣨�ú�a�Ĵ���ʽ��ʾ����
(2)˵��ֱ�������������������㣻
(3)ֱ���������ߵ���һ�������ΪN.
������1��a��һ![]() �����߶�MN���ȵ�ȡֵ��Χ��
�����߶�MN���ȵ�ȡֵ��Χ��
�����QMN�������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���BCA��90�㣬AC��BC����D��BC���е㣬��F���߶�AD�ϣ�DF��CD��BF��CA��E�㣬����A��DA�Ĵ��߽�CF���ӳ����ڵ�G�����н��ۣ���CF2��EFBF����AG��2DC����AE��EF����AFEC��EFEB��������ȷ�Ľ����У�������
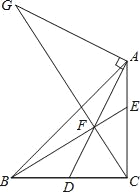
A. �٢ڢ� B. �٢ڢ� C. �٢ۢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,����ֱ��������ֽƬABC �У���C=90��,��ֽƬ��EF ���ۺ�Aǡ������BC �ϵĵ�D������CE=I,AC=4,�����н���һ����ȷ�ĸ����ǣ� ��
�١�CDE= ��DFB ;��BD > CE ;��BC= ![]() CD ;�ܡ�DCE ����BDF ���ܳ����.
CD ;�ܡ�DCE ����BDF ���ܳ����.

A. 1�� B. 2�� C. 3�� D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
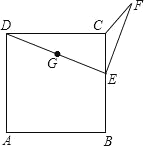
����Ŀ����ͼ����֪������ ABCD �ı߳�Ϊ 10��E �� BC �����˶���ȡ DE ���е� G��EG �Ƶ� E ˳ʱ����ת90��� EF���� CE ��Ϊ����ʱ��A��C��F ������һ��ֱ���ϣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com