
【题目】已知直线y=2x+m与抛物线y=ax2+ax+b有一个公共点M(1,0),且a<b.
(1)求抛物线顶点Q的坐标(用含a的代数式表示);
(2)说明直线与抛物线有两个交点;
(3)直线与抛物线的另一个交点记为N.
①若-1≤a≤一![]() ,求线段MN长度的取值范围;
,求线段MN长度的取值范围;
②求△QMN面积的最小值.
【答案】(1)(-![]() ,-
,-![]() )(2)证明见解析(3)
)(2)证明见解析(3)![]()
【解析】分析: (1)把M点坐标代入抛物线解析式可得到b与a的关系,可用a表示出抛物线解析式,化为顶点式可求得其顶点坐标;
(2)由直线解析式可先求得m的值,联立直线与抛物线解析式,消去y,可得到关于x的一元二次方程,再判断其判别式大于0即可;
(3)①由(2)的方程,可求得N点坐标,利用勾股定理可求得MN2,利用二次函数性质可求得MN长度的取值范围;②设抛物线对称轴交直线与点E,则可求得E点坐标,利用S△QMN=S△QEN+S△QEM可用a表示出△QMN的面积,再整理成关于a的一元二次方程,利用判别式可得其面积的取值范围,可求得答案
详解:
(1)∵M(1,0),
∴b=-2a,
∴y=ax2+ax+b
=ax2+ax-2a
= a(x+![]() )2-
)2-![]()
∴顶点Q的坐标为(-![]() ,-
,-![]() ).
).
(2)由直线y=2x+m经过点M(1,0),可得m=-2.
∴y=2x-2
∴ax2+(a-2)x-2a+2=0
∴△=(a-2)2-4×a×(-2a+2)=(3a-2)2
∵2a +b=0,a<b
∴a<0
∴△>0
∴方程有两个不相等的实数根,
∴直线与抛物线有两个交点.
(3)把y=2x-2代入y=ax2+ax-2a,得ax2+(a-2)x-2a+2=0,
即x2+(1-![]() )x-2+
)x-2+![]() =0,
=0,
∴(x-1)(x+2-![]() )=0,
)=0,
解得x1=1,x2 =![]() -2,
-2,
∴点N(![]() -2,
-2,![]() -6).
-6).
(i)根据勾股定理得,
MN2=[(![]() -2)-1]2+(
-2)-1]2+(![]() -6)2=20(
-6)2=20(![]() )2,
)2,
∵-1≤a≤-![]() ,
,
∴-2≤![]() ≤-1,
≤-1,
∴![]() <0,
<0,
∴MN=2![]() (
(![]() )=3
)=3![]() ,
,
∴5![]() ≤MN≤7
≤MN≤7![]() .
.
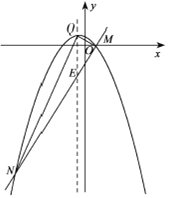
(ii)作直线x=-![]() 交直线y=2x-2于点E,
交直线y=2x-2于点E,
把x=-![]() 代入y=2x-2得,y=-3,
代入y=2x-2得,y=-3,
即E(-![]() ,-3),
,-3),
∵M(1,0),N(![]() -2,
-2,![]() -6),且由(2)知a<0,
-6),且由(2)知a<0,
∴S△QMN =S△QEN+S△QEM= ![]() =
=![]() ,
,
即27a2+(8S-54)a+24=0,
∵关于a的方程有实数根,
∴△=(8S-54)2-4×27×24≥0,
即(8S-54)2≥(36![]() )2,
)2,
又∵a<0,
∴S=![]() >
>![]() ,
,
∴8S-54>0,
∴8S-54≥36![]() ,即S≥
,即S≥![]() ,
,
当S=![]() 时,由方程可得a=-
时,由方程可得a=-![]() 满足题意.
满足题意.
∴△QMN面积的最小值为![]() .
.
点睛: 本题为二次函数的综合应用,涉及函数图象的交点、二次函数的性质、根的判别式、勾股定理、三角形的面积等知识.在(1)中由M的坐标得到b与a的关系是解题的关键,在(2)中联立两函数解析式,得到关于x的一元二次方程是解题的关键,在(3)中求得N点的坐标是解题的关键,在最后一小题中用a表示出△QMN的面积是解题的关键.本题考查知识点较多,综合性较强,难度较大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知数轴上三点A,O,B表示的数分别为6,0,-4,动点P从A出发,以每秒6个单位的速度沿数轴向左匀速运动.
(1)当点P到点A的距离与点P到点B的距离相等时,点P在数轴上表示的数是 ;
(2)另一动点R从B出发,以每秒4个单位的速度沿数轴向左匀速运动,若点P、R同时出发,问点P运动多少时间追上点R?
(3)若M为AP的中点,N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若发生变化,请你说明理由;若不变,请你画出图形,并求出线段MN的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c (a≠0)的图象如图所示,对称轴是x=-1.下列结论:①ab>0;②b2>4ac;③a-b+2c<0;④8a+c<0.其中正确的是( )

A. ③④ B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
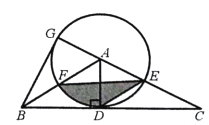
【题目】如图,在△ABC中,过点A作AD⊥BC,垂足为点D,以AD为半径的⊙A分别与边AC、AB交于点E和点F,DE∥AB,延长CA交⊙A于点G,连接BG.
(1)求证:BG是⊙A的切线;
(2)若∠ACB=30°,AD=3,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
如图,在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF相交于点G,则下列结论不正确的是( )
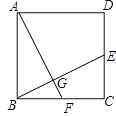
A.BE=AF B.∠DAF=∠BEC C.∠AFB+∠BEC=90° D.AG⊥BE
查看答案和解析>>
科目:初中数学 来源: 题型:
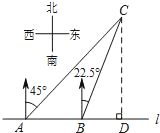
【题目】如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为_____km(精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
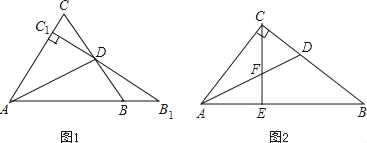
【题目】如图(1)所示:等边△ABC中,线段AD为其内角角平分线,过D点的直线B1C1⊥AC于C1交AB的延长线于B1.
(1)请你探究:![]() ,
,![]() 是否都成立?
是否都成立?
(2)请你继续探究:若△ABC为任意三角形,线段AD为其内角角平分线,请问![]() 一定成立吗?并证明你的判断.
一定成立吗?并证明你的判断.
(3)如图(2)所示Rt△ABC中,∠ACB=90,AC=8,AB=![]() ,DE∥AC交AB于点E,试求
,DE∥AC交AB于点E,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
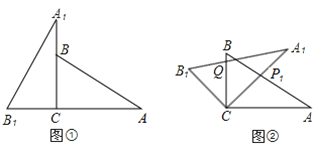
【题目】将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.
(1)将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;
(2)在图②中,若AP1=2,则CQ等于多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为传承中华优秀传统文化,某校团委组织了一次全校![]() 名学生参加的“汉字书写”大赛,为了解本次大赛的成绩,校团委随机抽取了其中
名学生参加的“汉字书写”大赛,为了解本次大赛的成绩,校团委随机抽取了其中![]() 名学生的成绩(成绩
名学生的成绩(成绩![]() 取整数,总分
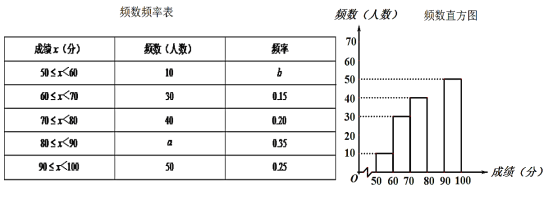
取整数,总分![]() 分)作为样本进行统计,制成如下不完整的统计图表:
分)作为样本进行统计,制成如下不完整的统计图表:
根据所给信息,解答下列问题:
(1)![]() _____,
_____,![]() ______;
______;
(2)补全频数直方图;
(3)这![]() 名学生成绩的中位数会落在______分数段;
名学生成绩的中位数会落在______分数段;
(4)若成绩在![]() 分以上(包括
分以上(包括![]() 分)为“优”等,请你估计该校参加本次比赛的
分)为“优”等,请你估计该校参加本次比赛的![]() 名学生中成绩为“优”等的有多少人。
名学生中成绩为“优”等的有多少人。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com