
【题目】星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题.
(1)玲玲到达离家最远的地方是什么时间?离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)她骑车速度最快是在什么时候?车速多少?
(4)玲玲全程骑车的平均速度是多少?
【答案】
(1)解:观察图象可知:玲玲到离家最远的地方需要12小时,此时离家30千米
(2)解:10点半时开始第一次休息;休息了半小时
(3)解:玲玲郊游过程中,各时间段的速度分别为: 9~10时,速度为10÷(10﹣9)=10千米/时; 10~10.5时,速度约为(17.5﹣10)÷(10.5﹣10)=15千米/小时; 10.5~11时,速度为0; 11~12时,速度为(30﹣17.5)÷(12﹣11)=12.5千米/小时; 12~13时,速度为0; 13~15时,在返回的途中,速度为:30÷(15﹣13)=15千米/小时; 可见骑行最快有两段时间:10~10.5时;13~15时.两段时间的速度都是15千米/小时.速度为:30÷(15﹣13)=15千米/小时
(4)解:玲玲全程骑车的平均速度为:(30+30)÷(15﹣9)=10千米/小时
【解析】(1)由图像可知,玲玲到离家最远的地方需要12小时,此时离家30千米;(2)由图像可知,10点半时开始第一次休息;休息了半小时;(3)由图像可知,骑行最快有两段时间:10~10.5时;13~15时.两段时间的速度都是15千米/小时;(4)玲玲全程骑车的平均速度是:总路程![]() 总时间,即:(30+30)÷(15﹣9)。
总时间,即:(30+30)÷(15﹣9)。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】从甲地到乙地的铁路路程约为615千米,高铁速度为300千米/小时,直达;动车速度为200千米/小时,行驶180千米后,中途要停靠徐州10分钟,若动车先出发半小时,两车与甲地之间的距离y(千米)与动车行驶时间x(小时)之间的函数图象为( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AD、FC、EB两两相交,连接AB、CD、EF,则∠A+∠B+∠C+∠D+∠E+∠F=( ) 
A.360°
B.240°
C.200°
D.180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的距离分别为y甲(km)、y乙(km),甲车行驶的时间为x(h),y甲、y乙与x之间的函数图像如图所示,现有4种说法:①甲车的速度是80km/h;②乙车休息了1小时;③两车相距80km时,甲车行驶了3小时;④乙车两次行驶的速度相同.上述说法正确的有个. 
查看答案和解析>>
科目:初中数学 来源: 题型:
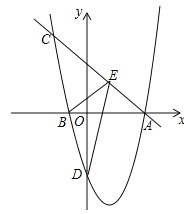
【题目】如图,抛物线![]() (a≠0)与x轴交于A(4,0)、B(﹣1,0)两点,过点A的直线y=﹣x+4交抛物线于点C.
(a≠0)与x轴交于A(4,0)、B(﹣1,0)两点,过点A的直线y=﹣x+4交抛物线于点C.
(1)求此抛物线的解析式;
(2)在直线AC上有一动点E,当点E在某个位置时,使△BDE的周长最小,求此时E点坐标;
(3)当动点E在直线AC与抛物线围成的封闭线A→C→B→D→A上运动时,是否存在使△BDE为直角三角形的情况,若存在,请直接写出符合要求的E点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,则下列说法正确的是( ) 
A.AD垂直FE
B.AD平分EF
C.EF垂直平分AD
D.AD垂直平分EF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com