练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】若|a﹣1|+（b+3）2＝0，则a+b＝（　　）

    A. ﹣4 B. ﹣2 C. 2 D. 4

    【答案】B

    【解析】

    根据非负数的性质列式求出a、b的值，然后代入代数式进行计算即可得解．

    由题意得，a1=0，b+3=0，

    解得a=1，b=3，

    所以,a+b=1+(3)=2.

    故答案选：B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】星期天，玲玲骑自行车到郊外游玩，她离家的距离与时间的关系如图所示，请根据图象回答下列问题．
    （1）玲玲到达离家最远的地方是什么时间？离家多远？
    （2）她何时开始第一次休息？休息了多长时间？
    （3）她骑车速度最快是在什么时候？车速多少？
    （4）玲玲全程骑车的平均速度是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后，将其裁成四个相同的等腰梯形（如图甲），然后拼成一个平行四边形（如图乙）．那么通过计算两个图形阴影部分的面积，可以验证成立的公式为（ ）
    A.a2﹣b2=（a﹣b）2
    B.（a+b）2=a2+2ab+b2
    C.（a﹣b）2=a2﹣2ab+b2
    D.a2﹣b2=（a+b）（a﹣b）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某风景区对5个旅游景点的游客人数进行了统计，有关数据如下表：

    景点

    A

    B

    C

    D

    E

    票价（元）

    10

    10

    15

    20

    25

    平均日人数（千人）

    1

    1

    2

    3

    2


    （1）如果这个星期天你去此风景区游玩，小刚、小明也去了，你在哪个景点遇见他们两个的机会较大？为什么？
    （2）如果到了这个风景区，你不想把这几个景点全部参观完，但又不知选哪一个，于是你想出一个主意：抓阄，那么，你抓出哪种票价的机会较大有多大？此时你参观哪个景点的机会较大？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点M的坐标是（5，4），⊙M与y轴相切于点C，与x轴相交于A、B两点．

    （1）则点A、B、C的坐标分别是A（__，__），B（__，__），C（__，__）；

    （2）设经过A、B两点的抛物线解析式为，它的顶点为F，求证：直线FA与⊙M相切；

    （3）在抛物线的对称轴上，是否存在点P，且点P在x轴的上方，使△PBC是等腰三角形．如果存在，请求出点P的坐标；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：
    （1）（﹣16 ）﹣（﹣10 ）﹣（+1 ）
    （2）（﹣ ）×（﹣1 ）÷（﹣2 ）
    （3）（﹣2）2×6﹣（﹣2）3÷4
    （4）（4a2b﹣5ab2）﹣（3a2b﹣4ab2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

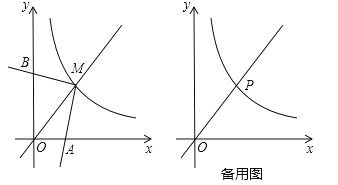
    【题目】如图，反比例函数（x＞0）的图象与直线y=x交于点M，∠AMB=90°，其两边分别与两坐标轴的正半轴交于点A，B，四边形OAMB的面积为6．

    （1）求k的值；

    （2）点P在反比例函数（x＞0）的图象上，若点P的横坐标为3，∠EPF=90°，其两边分别与x轴的正半轴，直线y=x交于点E，F，问是否存在点E，使得PE=PF？若存在，求出点E的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

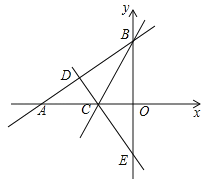
    【题目】如图，在平面直角坐标系中，已知Rt△AOB的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，且OA、OB的长满足，∠ABO的平分线交x轴于点C过点C作AB的垂线，垂足为点D，交y轴于点E．

    （1）求线段AB的长；

    （2）求直线CE的解析式；

    （3）若M是射线BC上的一个动点，在坐标平面内是否存在点P，使以A、B、M、P为顶点的四边形是矩形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若a2+b+5=0，则代数式3a2+3b+10=0的值为（ ）

    A. 25 B. 5 C. -5 D. 0

    查看答案和解析>>

    同步练习册答案