
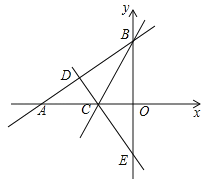
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪Rt��AOB����ֱ�DZ�OA��OB�ֱ���x��ĸ������y����������ϣ���OA��OB�ij�����![]() ����ABO��ƽ���߽�x���ڵ�C����C��AB�Ĵ��ߣ�����Ϊ��D����y���ڵ�E��
����ABO��ƽ���߽�x���ڵ�C����C��AB�Ĵ��ߣ�����Ϊ��D����y���ڵ�E��
��1�����߶�AB�ij���
��2����ֱ��CE�Ľ���ʽ��
��3����M������BC�ϵ�һ�����㣬������ƽ�����Ƿ���ڵ�P��ʹ��A��B��M��PΪ������ı����Ǿ��Σ������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��10����2��![]() ����3�����ڣ�P����3��10����P��3��2����
����3�����ڣ�P����3��10����P��3��2����
��������
�����������1�����ݷǸ����������������OA��OB�ij���Ȼ����ݹ��ɶ������AB�ij���
��2��֤����ACD�ס�AOB���õ�OC=CD����������ACD�ס�AOB���������������εĶ�Ӧ�ߵı�������OC�ij����Ӷ����C�����꣬����CD��AB�����AB�Ľ���ʽ���������CE�Ľ���ʽ��
��3��M�ǹ�A�Ҵ�ֱ��AB��ֱ����BC�Ľ��㣬�������M�����꣬Ȼ��ֳ��ı���ABPM�Ǿ��κ�APBM�Ǿ�����������������ۣ�
�����������1����![]() ����OA=8��OB=6����ֱ����AOB�У�AB=
����OA=8��OB=6����ֱ����AOB�У�AB=![]() =
=![]() =10��
=10��
��2������OBC����DBC�У��ߡ�OBC=��DBC��BC=BC����BOC=��BDC�����OBC�ա�DBC����OC=CD����OC=x����AC=8��x��CD=x���ߡ�ACD����ABO�У���CAD=��BAO����ADC=��AOB=90�㣬���ACD�ס�AOB����![]() ����
����![]() ����ã�x=3����OC=3����C�������ǣ���3��0������AB�Ľ���ʽ��
����ã�x=3����OC=3����C�������ǣ���3��0������AB�Ľ���ʽ��![]() �������������
�������������![]() ����ã�
����ã� ����ֱ��AB�Ľ���ʽ��
����ֱ��AB�Ľ���ʽ��![]() ��
��
��CD�Ľ���ʽ��![]() ����
����![]() ����
����![]() ����ֱ��CE�Ľ���ʽ��
����ֱ��CE�Ľ���ʽ��![]() ��
��
��3����ֱ��BC�Ľ���ʽ��![]() ������
������![]() ����ã�
����ã�![]() ����ֱ��BC�Ľ���ʽ��
����ֱ��BC�Ľ���ʽ��![]() ��
��
�辭��A����AB��ֱ��ֱ�ߵĽ���ʽ��![]() ����
����![]() ����ã�
����ã�![]() ��
��
���A����AB��ֱ��ֱ�ߵĽ���ʽ��![]() ��
��
��������ã�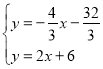 ����ã�
����ã�![]() ����M�������ǣ�
����M�������ǣ�![]() ��
��![]() ����
����
�����ı���ABPM�Ǿ���ʱ���߶�AP���е����߶�BM���е��غϣ���P��x��y������A����8��0����B��0��6����M��![]() ��
��![]() ���������е����깫ʽ�У�
���������е����깫ʽ�У�![]() ��
��![]() �����x=3��y=2����P��3��2����
�����x=3��y=2����P��3��2����
����APBM�Ǿ���ʱ���߶�AB���е����߶�PM���е��غ���P��x��y������A����8��0����B��0��6����M��![]() ��
��![]() ���������е����깫ʽ�У�
���������е����깫ʽ�У�![]() ��
��![]() �����x=��3��y=10����P����3��10����
�����x=��3��y=10����P����3��10����
��������������P��3��2����P����3��10������������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD�ǡ�ABC�Ľ�ƽ���ߣ�DE��DF�ֱ��ǡ�ABD�͡�ACD�ĸߣ�������˵����ȷ���ǣ� �� 
A.AD��ֱFE
B.ADƽ��EF
C.EF��ֱƽ��AD
D.AD��ֱƽ��EF
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����|a��1|+��b+3��2��0����a+b����������
A. ��4 B. ��2 C. 2 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�AB=AC=9cm��BC=6cm��DΪBC���е㣬����P��B���������ÿ��1cm���ٶ���B��A��C��·���˶���Cֹͣ�����˶�ʱ��Ϊt����D��P�����ֱ�߽���ABC���ܳ��ֳ��������֣�������һ��������һ���ֵ�2�������ʱt��ֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������
��1��������x3��2+��2x2��3+��x��3����2
��2�����㣺 ![]() ��
�� ![]() +��
+�� ![]() ��1��0 ��
��1��0 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڶ�ij�������ĵ������ռ����������ݣ�����Ϊ���ܹ���ӳ�û�������������ͳ�����ǣ�������
���� | 13 | 14 | 15 | 25 | 28 | 30 | 35 | ���� |
���� | 30 | 533 | 17 | 12 | 20 | 9 | 2 | 3 |
A. ƽ���� B. ���� C. ���� D. ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x��һԪ���η���x2��2x+m��0��������ȵ�ʵ��������m��ֵ�ǣ�������
A.��1B.0C.1D.2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�������߸���һ�������ֱ��30�ߺ�20�ߣ������ľ�����50�ߣ�ÿ�����������϶�ͣ��һֻ��Ȼ����ֻ��ͬʱ����ˮ�����γ�һ���㣬�������̷�ȥץ�㣬�ٶ���ͬ������ͬʱ����Ŀ�꣮����������ֵĵط��뿪�Ƚϸߵ����ľ���Ϊ�ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʽ�ֽ���ȷ����( )
A. ab+ac+ad+1=a(b+c+d)+1
B. (x+1)(x+2)=x2+3x+2
C. a3+3a2b+a=a(a2+3ab+1)
D. x2-y2=(x+y)(y-x)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com