练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】若关于x的一元二次方程x2﹣2x+m＝0有两个相等的实数根，则m的值是（　　）

    A.﹣1B.0C.1D.2

    【答案】C

    【解析】

    根据题意可得一元二次方程根的判别式值等于0，求出m即可.

    解：∵关于x的一元二次方程x2﹣2x+m＝0有两个相等的实数根，

    ∴△＝b2﹣4ac＝（﹣2）2﹣4×1×m＝4﹣4m＝0，

    ∴m＝1．

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后，将其裁成四个相同的等腰梯形（如图甲），然后拼成一个平行四边形（如图乙）．那么通过计算两个图形阴影部分的面积，可以验证成立的公式为（ ）
    A.a2﹣b2=（a﹣b）2
    B.（a+b）2=a2+2ab+b2
    C.（a﹣b）2=a2﹣2ab+b2
    D.a2﹣b2=（a+b）（a﹣b）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

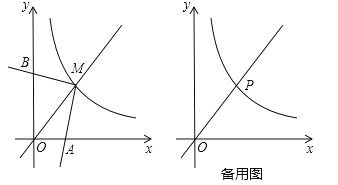
    【题目】如图，反比例函数（x＞0）的图象与直线y=x交于点M，∠AMB=90°，其两边分别与两坐标轴的正半轴交于点A，B，四边形OAMB的面积为6．

    （1）求k的值；

    （2）点P在反比例函数（x＞0）的图象上，若点P的横坐标为3，∠EPF=90°，其两边分别与x轴的正半轴，直线y=x交于点E，F，问是否存在点E，使得PE=PF？若存在，求出点E的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

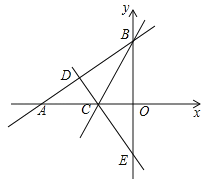
    【题目】如图，在平面直角坐标系中，已知Rt△AOB的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，且OA、OB的长满足，∠ABO的平分线交x轴于点C过点C作AB的垂线，垂足为点D，交y轴于点E．

    （1）求线段AB的长；

    （2）求直线CE的解析式；

    （3）若M是射线BC上的一个动点，在坐标平面内是否存在点P，使以A、B、M、P为顶点的四边形是矩形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若x2+2(m-3)x+16是完全平方式，则m的值等于（ ）

    A. 3 B. -5 C. -7或1 D. 7或-1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，抛物线与x轴交于A，B，与y轴交于C，抛物线的顶点为D，直线l过C交x轴于E（4，0）．

    （1）写出D的坐标和直线l的解析式；

    （2）P（x，y）是线段BD上的动点（不与B，D重合），PF⊥x轴于F，设四边形OFPC的面积为S，求S与x之间的函数关系式，并求S的最大值；

    （3）点Q在x轴的正半轴上运动，过Q作y轴的平行线，交直线l于M，交抛物线于N，连接CN，将△CMN沿CN翻转，M的对应点为M′．在图2中探究：是否存在点Q，使得M′恰好落在y轴上？若存在，请求出Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列变形正确的是（ ）
    A.4x﹣5=3x+2变形得4x﹣3x=﹣2+5
    B.﹣3x=2变形得
    C.3（x﹣1）=2（x+3）变形得3x﹣1=2x+6
    D. 变形得4x﹣6=3x+18

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若a2+b+5=0，则代数式3a2+3b+10=0的值为（ ）

    A. 25 B. 5 C. -5 D. 0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现有甲、乙两个体育用品商店出售乒乓球拍和乒乓球，球拍每块价格为48元，乒乓球每个价格为2元，已知甲店制定的优惠方法是买一块球拍送6个乒乓球，乙店按总价的90%收费，某球队需要买球拍4块，乒乓球若干（不少于24个）．
    （1）当购买多少个乒乓球时，两个商店的收费一样多？
    （2）当需要购买240个乒乓球时，选择哪家商店购买更优惠？请说明理由．

    查看答案和解析>>

    同步练习册答案