
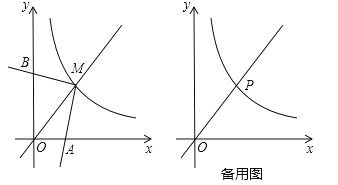
【题目】如图,反比例函数![]() (x>0)的图象与直线y=x交于点M,∠AMB=90°,其两边分别与两坐标轴的正半轴交于点A,B,四边形OAMB的面积为6.
(x>0)的图象与直线y=x交于点M,∠AMB=90°,其两边分别与两坐标轴的正半轴交于点A,B,四边形OAMB的面积为6.
(1)求k的值;
(2)点P在反比例函数![]() (x>0)的图象上,若点P的横坐标为3,∠EPF=90°,其两边分别与x轴的正半轴,直线y=x交于点E,F,问是否存在点E,使得PE=PF?若存在,求出点E的坐标;若不存在,请说明理由.
(x>0)的图象上,若点P的横坐标为3,∠EPF=90°,其两边分别与x轴的正半轴,直线y=x交于点E,F,问是否存在点E,使得PE=PF?若存在,求出点E的坐标;若不存在,请说明理由.
【答案】(1)6;(2)E(4,0)或E(6,0).
【解析】
试题分析:(1)过点M作MC⊥x轴于点C,MD⊥y轴于点D,根据AAS证明△AMC≌△BMD,那么S四边形OCMD=S四边形OAMB=6,根据反比例函数比例系数k的几何意义得出k=6;
(2)先根据反比例函数图象上点的坐标特征求得点P的坐标为(3,2).再分两种情况进行讨论:①如图2,过点P作PG⊥x轴于点G,过点F作FH⊥PG于点H,交y轴于点K.根据AAS证明△PGE≌△FHP,进而求出E点坐标;②如图3,同理求出E点坐标.
试题解析:(1)如图1,过点M作MC⊥x轴于点C,MD⊥y轴于点D,则∠MCA=∠MDB=90°,∠AMC=∠BMD,MC=MD,∴△AMC≌△BMD,∴S四边形OCMD=S四边形OAMB=6,∴k=6;
(2)存在点E,使得PE=PF.
由题意,得点P的坐标为(3,2).
①如图2,过点P作PG⊥x轴于点G,过点F作FH⊥PG于点H,交y轴于点K.
∵∠PGE=∠FHP=90°,∠EPG=∠PFH,PE=PF,∴△PGE≌△FHP,∴PG=FH=2,FK=OK=3﹣2=1,GE=HP=2﹣1=1,∴OE=OG+GE=3+1=4,∴E(4,0);
②如图3,过点P作PG⊥x轴于点G,过点F作FH⊥PG于点H,交y轴于点K.
∵∠PGE=∠FHP=90°,∠EPG=∠PFH,PE=PF,∴△PGE≌△FHP,∴PG=FH=2,FK=OK=3+2=5,GE=HP=5﹣2=3,∴OE=OG+GE=3+3=6,∴E(6,0).
综上所述,E(4,0)或E(6,0).


科目:初中数学 来源: 题型:
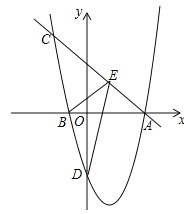
【题目】如图,抛物线![]() (a≠0)与x轴交于A(4,0)、B(﹣1,0)两点,过点A的直线y=﹣x+4交抛物线于点C.
(a≠0)与x轴交于A(4,0)、B(﹣1,0)两点,过点A的直线y=﹣x+4交抛物线于点C.
(1)求此抛物线的解析式;
(2)在直线AC上有一动点E,当点E在某个位置时,使△BDE的周长最小,求此时E点坐标;
(3)当动点E在直线AC与抛物线围成的封闭线A→C→B→D→A上运动时,是否存在使△BDE为直角三角形的情况,若存在,请直接写出符合要求的E点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“六一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法不正确的是( )
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”区域的次数m | 68 | 108 | 140 | 355 | 560 | 690 |
落在“铅笔”区域的频率 | 0.68 | 0.72 | 0.70 | 0.71 | 0.70 | 0.69 |

A.当n很大时,估计指针落在“铅笔”区域的频率大约是0.70
B.假如你去转动转盘一次,获得铅笔的概率大约是0.70
C.如果转动转盘2000次,指针落在“文具盒”区域的次数大约有600次
D.转动转盘10次,一定有3次获得文具盒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A、∠B、∠C的对边分别是a、b、c,AB=8,BC=15,CA=17,则下列结论不正确的是( )
A.△ABC是直角三角形,且AC为斜边
B.△ABC是直角三角形,且∠ABC=90°
C.△ABC的面积是60
D.△ABC是直角三角形,且∠A=60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC=9cm,BC=6cm,D为BC的中点,动点P从B点出发,以每秒1cm的速度沿B→A→C的路线运动到C停止.设运动时间为t,过D、P两点的直线将△ABC的周长分成两个部分,若其中一部分是另一部分的2倍,则此时t的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为实现教育均衡发展,打造新优质学校,瑶海区计划对A、B两类薄弱学校全部进行改造,根据预算,共需资金1575万元.改造一所A类学校和两所B类学校共需资金230万元;改造两所A类学校和一所B类学校共需资金205万元,求改造一所A类学校和一所B类学校所需的资金分别是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com