
【题目】解方程组或不等式组.
(1)![]()
(2)![]() .
.
【答案】
(1)解: ![]() ,
,
②﹣①得2y=7,
则y= ![]() ,
,
把y= ![]() 代入①得7x+7=8,
代入①得7x+7=8,
解得x= ![]() ,
,
则方程组的解是 ![]()
(2)解: ![]() ,
,
解(1)得x≥﹣1,
解(2)得x≥ ![]() ,
,
则不等式组的解集是x≥ ![]()
【解析】①利用加减法即可求解;②首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.
【考点精析】本题主要考查了解二元一次方程组和一元一次不等式组的解法的相关知识点,需要掌握二元一次方程组:①代入消元法;②加减消元法;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )才能正确解答此题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
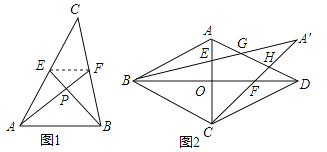
【题目】尤秀同学遇到了这样一个问题:如图1所示,已知AF,BE是△ABC的中线,且AF⊥BE,垂足为P,设BC=a,AC=b,AB=c.
求证:![]() .
.
该同学仔细分析后,得到如下解题思路:
先连接EF,利用EF为△ABC的中位线得到△EPF∽△BPA,故![]() ,设PF=m,PE=n,用m,n把PA,PB分别表示出来,再在Rt△APE,Rt△BPF中利用勾股定理计算,消去m,n即可得证.
,设PF=m,PE=n,用m,n把PA,PB分别表示出来,再在Rt△APE,Rt△BPF中利用勾股定理计算,消去m,n即可得证.
(1)请你根据以上解题思路帮尤秀同学写出证明过程.
(2)利用题中的结论,解答下列问题:
在边长为3的菱形ABCD中,O为对角线AC,BD的交点,E,F分别为线段AO,DO的中点,连接BE,CF并延长交于点M,BM,CM分别交AD于点G,H,如图2所示,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保护视力,学校计划开展“爱眼护眼”视力保健活动,为使活动更具有实效性,先对学生视力情况进行调查,随机抽取40名学生,检查他们的视力,并绘制不完整的直方图(数据包括左端点不包括右端点,精确到0.1),请结合直方图的信息解答下列问题: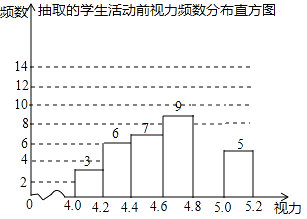
(1)统计图中,4.8≤x<5.0的学生数是人;
(2)将频数分布直方图补充完整;
(3)若绘制“学生视力扇形统计图”,视力达到4.8及以上为达标,则视为达标学生所对应扇形的圆心角度数为°;
(4)若全校共有800名学生,则视力达标的学生估计有名.
查看答案和解析>>
科目:初中数学 来源: 题型:
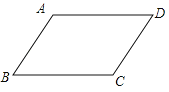
【题目】如图,在ABCD中,已知AD>AB.
(1)实践与操作:作∠BAD的平分线交BC于点E,在AD上截取AF=AB,连接EF;(要求:尺规作图,保留作图痕迹,不写作法)
(2)猜想并证明:猜想四边形ABEF的形状,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【阅读】
我们分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,
其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M﹣N,若M﹣N>0,则M>N;若M﹣N=0,则M=N;若M﹣N<0,则M<N.
【运用】
利用“作差法”解决下列问题:
(1)小丽和小颖分别两次购买同一种商品,小丽两次都买了m千克商品,小颖两次购买商品均花费n元,已知第一次购买该商品的价格为a元/千克,第二次购买该商品的价格为b元/千克(a,b是整数,且a≠b),试比较小丽和小颖两次所购买商品的平均价格的高低.
(2)奶奶提一篮子玉米到集贸市场去兑换大米,每2kg玉米兑换1kg大米,商贩用秤称得连篮子带玉米恰好20kg,于是商贩连篮子带大米给奶奶共10kg,在这个过程中谁吃了亏?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区有一块面积为196m2的正方形空地,开发商计划在此空地上建一个面积为100m2的长方形花坛,使长方形的长是宽的2倍.请你通过计算说明开发商能否实现这个愿望?(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈7.070)
≈7.070)
查看答案和解析>>
科目:初中数学 来源: 题型:
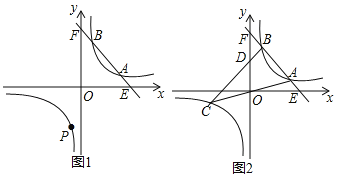
【题目】已知:一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() )的图象相交于A,B两点(A在B的右侧).
)的图象相交于A,B两点(A在B的右侧).
(1)当A(4,2)时,求反比例函数的解析式及B点的坐标;
(2)在(1)的条件下,反比例函数图象的另一支上是否存在一点P,使△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)当A(a,﹣2a+10),B(b,﹣2b+10)时,直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.若![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锐角三角形ABC中(AB>AC),AH⊥BC,垂足为H,E、D、F分别是各边的中点,则四边形EDHF是( ) 
A.梯形
B.等腰梯形
C.直角梯形
D.矩形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com