
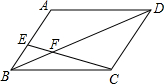
 如图,在?ABCD中,E在AB上,CE、BD交于F,若AE:BE=4:3,且BF=2,则BD=
如图,在?ABCD中,E在AB上,CE、BD交于F,若AE:BE=4:3,且BF=2,则BD= 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
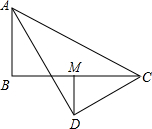 在Rt△ABC中,∠B=90°,AD平分∠BAC,CD⊥AD,垂足为D,DM⊥BC.
在Rt△ABC中,∠B=90°,AD平分∠BAC,CD⊥AD,垂足为D,DM⊥BC.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| AD |
| CD |
| BC |
| BE |
| 4 |
| 3 |
| AD |
| CD |
查看答案和解析>>
科目:初中数学 来源: 题型:
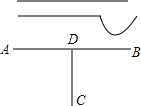 水质卫生状况关系到千家万户,是重大民生工程,泗阳县城乡供水一体化模式的实践被群众称为“德政工程”、“惠民工程”.如图,2014年计划把大运河(AB)中的水引到水厂C中,可先过C作CD⊥AB,垂足为D,然后沿CD开渠,则能使所开的渠道最短,这种设计方案的根据是
水质卫生状况关系到千家万户,是重大民生工程,泗阳县城乡供水一体化模式的实践被群众称为“德政工程”、“惠民工程”.如图,2014年计划把大运河(AB)中的水引到水厂C中,可先过C作CD⊥AB,垂足为D,然后沿CD开渠,则能使所开的渠道最短,这种设计方案的根据是查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 5 |
| 13 |
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com