
分析 (1)由四边形ABCD是菱形,可得AB=AD,又由平行四边形ABCD的两边AB,AD的长是关于x的方程:x2-3ax+3a-1=0的两个实数根,可得x2-3ax+3a-1=0有相等的实数根,即△=0,则可求得a的值,继而求得答案;
(2)首先将方程的一个根2,代入x2-3ax+3a-1=0,即可求得a的值,继而求得答案.
解答 解:(1)∵四边形ABCD是菱形,
∴AB=AD,
∵平行四边形ABCD的两边AB,AD的长是关于x的方程:x2-3ax+3a-1=0的两个实数根,
∴△=(-3a)2-4×(3a-1)=9a2-12a+4=0,
解得:a=$\frac{2}{3}$,
∴当a=$\frac{2}{3}$时,四边形ABCD是菱形;
∴原方程为:x2-2x+1=0,
解得:x1=x2=1,
∴这时菱形的边长为:1;
(2)∵此方程的一个根是2,
∴22-6a+3a-1=0,
解得:a=1,
∴原方程为:x2-3x+2=0,
∴(x-2)(x-1)=0,
解得:x1=2,x2=1,
∴AB+BC=3,
∴平行四边形ABCD的周长是:6.
点评 此题考查了平行四边形的性质、菱形的性质以及根的判别式.注意由菱形的邻边相等,得到x2-3ax+3a-1=0有相等的实数根,即△=0是关键.


科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP、BD与CF相交于点H.给出下列结论:①△ABE≌△DCF;②DP2=PH•PB;③$\frac{FP}{PH}=\frac{3}{5}$;④$\frac{{S}_{△ABC}}{{S}_{△BDC}}=\frac{\sqrt{3}}{2}$,其中正确的是①②.
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP、BD与CF相交于点H.给出下列结论:①△ABE≌△DCF;②DP2=PH•PB;③$\frac{FP}{PH}=\frac{3}{5}$;④$\frac{{S}_{△ABC}}{{S}_{△BDC}}=\frac{\sqrt{3}}{2}$,其中正确的是①②.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
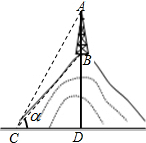 如图,在铅直高度为200m的小山上建有一座电视转播塔,某数学兴趣小组为测量电视转播塔的高度,在山脚的C处测得山顶B的仰角为30°(即∠BCD=30°),测得塔顶的仰角为45°(即∠ACD=45°),请根据以上数据求塔高AB.(精确到1m.备用数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
如图,在铅直高度为200m的小山上建有一座电视转播塔,某数学兴趣小组为测量电视转播塔的高度,在山脚的C处测得山顶B的仰角为30°(即∠BCD=30°),测得塔顶的仰角为45°(即∠ACD=45°),请根据以上数据求塔高AB.(精确到1m.备用数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC和过点O的两条互相垂直的直线x、y,画出△ABC关于直线x对称的△A′B′C′,再画出△A′B′C′关于直线y对称的△A″B″C″,观察△ABC与△A″B″C″,这两个三角形具有怎样的对称性?
如图,已知△ABC和过点O的两条互相垂直的直线x、y,画出△ABC关于直线x对称的△A′B′C′,再画出△A′B′C′关于直线y对称的△A″B″C″,观察△ABC与△A″B″C″,这两个三角形具有怎样的对称性?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知A、B两点的坐标分别为(2,0)、(0,2),⊙C的圆心坐标为(-1,0),半径为1.若D是⊙O上的一个动点,线段DA与y轴交于点E,则△ABE面积的最大值为( )
如图,已知A、B两点的坐标分别为(2,0)、(0,2),⊙C的圆心坐标为(-1,0),半径为1.若D是⊙O上的一个动点,线段DA与y轴交于点E,则△ABE面积的最大值为( )| A. | 2+$\sqrt{2}$ | B. | 2+$\frac{\sqrt{2}}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com