
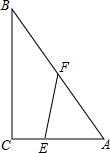
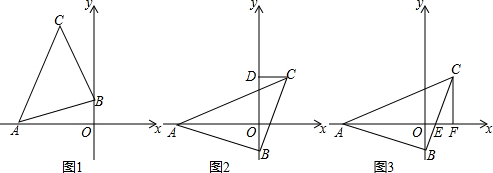
 ��ͼ����Rt��ABC�У���C=90��AC=3��BC=4����E��ֱ�DZ�AC�ϣ���E��A��C��������غϣ�����F��б��AB�ϣ���F��A��B��������غϣ���
��ͼ����Rt��ABC�У���C=90��AC=3��BC=4����E��ֱ�DZ�AC�ϣ���E��A��C��������غϣ�����F��б��AB�ϣ���F��A��B��������غϣ������� ��1������AE=x�õ�AF������F��FD��AC��D��Ȼ���ʾ��DF�����������ε�����г���������֮��Ĺ�ϵʽ���ɣ�
��2�����ݡ�AEF�����Ϊ$\frac{16}{5}$�г����̣��ⷽ�̼��ɣ�
��3������EFƽ��������ABC������г��й�x��һԪ���η��̣�����Ľ������弴���ж����ڣ�
��� 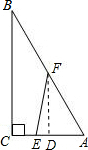 �⣺��1������ֱ��������ABC�У�AC=3��BC=4��
�⣺��1������ֱ��������ABC�У�AC=3��BC=4��
��AB=5��
��������ABC���ܳ�Ϊ12��
�֡�EFƽ��������ABC���ܳ���
��AE+AF=6����AE=x��
��AF=6-x��
����F��FD��AC��D��
��$\frac{DF}{AF}$=sinA=$\frac{BC}{AB}$��
��$\frac{DF}{6-x}$=$\frac{4}{5}$��
��DF=$\frac{4}{5}$��6-x����
��y=$\frac{1}{2}$AE•DF=$\frac{1}{2}$x•$\frac{4}{5}$��6-x��=-$\frac{2}{5}$x2+$\frac{12}{5}$x��1��x��3����
��2���ߡ�AEF�����Ϊ$\frac{16}{5}$��
��-$\frac{2}{5}$x2+$\frac{12}{5}$x=$\frac{16}{5}$��
���x=2��4��
4�������⣬��ȥ��
��x=2����AE�ij�Ϊ2��
��3��������EF���ڣ�
S��ABC=$\frac{1}{2}$BC•AC=$\frac{1}{2}$��4��3=6
��EFƽ�֡�ABC�������
����-$\frac{2}{5}$x2+$\frac{12}{5}$x=3��
��ã�x=$\frac{6��\sqrt{6}}{2}$��
��1��x��3
��xȡ$\frac{6-\sqrt{6}}{2}$��
��6-x=6-$\frac{6-\sqrt{6}}{2}$=$\frac{6+\sqrt{6}}{2}$��5��
�������⣬����������EF���ڣ���ʱAE=$\frac{6-\sqrt{6}}{2}$��
���� ���⿼����һԪ���η��̵�Ӧ�ü�����ʵ�������г����κ�����ϵʽ������Ĺؼ��Ǹ�����֪������ʾ���йص��߶εij���


 ��Կ���Ծ�ϵ�д�
��Կ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
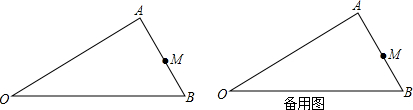
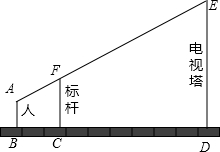 ��ͼ��ij����������Ա���˶���F��������������ͬһֱ���ϣ���֪�����۾������1.6�ף����Ϊ3.2�ף���BC=1�ף�CD=5�ף���������ĸ�ED=11.2��
��ͼ��ij����������Ա���˶���F��������������ͬһֱ���ϣ���֪�����۾������1.6�ף����Ϊ3.2�ף���BC=1�ף�CD=5�ף���������ĸ�ED=11.2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
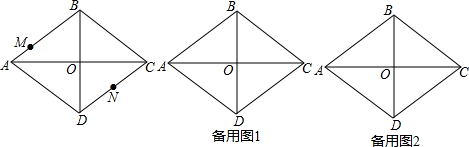
 ��ͼ��ij��̨���һ�ô����������3�״���B�������ζϣ����������ŵص�A��������C�ľ���Ϊ4�ף���ô������ĸ߶���8�ף�
��ͼ��ij��̨���һ�ô����������3�״���B�������ζϣ����������ŵص�A��������C�ľ���Ϊ4�ף���ô������ĸ߶���8�ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com