
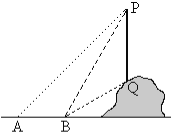
����Ŀ����ͼ��ʾ��ij��ѧ�С��Ҫ����ɽ���ϵĵ��߸�PQ�ĸ߶������Dz�ȡ�ķ����ǣ����ڵ����ϵĵ�A����ø˶��˵�P��������45��������ǰ�ߵ�B������ø˶��˵�P�˵˵�Q�����Ƿֱ���60���30������ʱֻ��Ҫ���AB�ij��Ⱦ���ͨ������������߸�PQ�ĸ߶�����ͬ�����ǵIJ�����������ͬ������������ʱ��ͼ������Ҫд�������˼·�������������ֵ������ͬ���������IJ�������������Ҫд������˼·��
���𰸡�![]() m��
m��
��������
����������ӳ�PQ��ֱ��AB�ڵ�E������AB�ij���Ϊm������ֱ����APE��ֱ����BPE�����������Ǻ�������PE��ʾ��AE��BE������AB=AE-BE�����г��������PE��ֵ������ֱ����BQE���������Ǻ������QE�ij�����PQ�ij��ȼ��������
���������ͬ�����ǵIJ���������
�ӳ�PQ��ֱ��AB�ڵ�E��
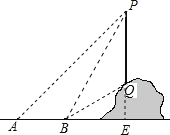
����AB�ij���Ϊm����
��ֱ����APE������A=45����
��AE=PE��
�ߡ�PBE=60��
���BPE=30��
��ֱ����BPE����BE=![]() PE��
PE��
��AB=AE-BE=m��
��PE-![]() PE=m��
PE=m��
��ã�PE=![]() m��
m��
��BE=![]() m-m=
m-m=![]() m��
m��
��ֱ����BEQ����QE=![]() BE=
BE=![]() ��
��![]() m��=
m��=![]() m��
m��
��PQ=PE-QE=![]() m-
m-![]() m=
m=![]() m��
m��


 ����˼ά�żӿ���ϵ�д�
����˼ά�żӿ���ϵ�д� �����Ծ�ϵ�д�
�����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC������ֱ�ΪA����3��5����B����4��2����C����1��4����ע��ÿ������ı߳���Ϊ1����λ���ȣ���
��1������ABC����ˮƽ��������ƽ��6����λ�á�A1B1C1���뻭����A1B1C1��
��2����������ABC����O������ĶԳƵġ�A2B2C2����ֱ��д�������ꣻ
��3����A1B1C1���A2B2C2�Ƿ�����ĶԳƣ����ǣ���д���Գ����ĵ����ꣻ�����ǣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֱ�������ε�һ��ֱ�DZ��غϵ��ţ���֪AC=BC=![]() +1����D=60����������б�ߵĽ���E��ֱ�DZ�BC�ľ����� ��
+1����D=60����������б�ߵĽ���E��ֱ�DZ�BC�ľ����� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
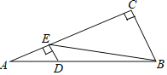
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬��A=30�㣬DΪAB��һ�㣬��AD��DB=1��3��DE��AC�ڵ�E������BE����tan��CBE��ֵ���ڣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���CDE�Ķ���C������ΪC��1����2������D�ĺ�����Ϊ![]() ������CDE�Ƶ�C��ת����CBO����D�Ķ�Ӧ��B��x�����һ������Ϊ��A��
������CDE�Ƶ�C��ת����CBO����D�Ķ�Ӧ��B��x�����һ������Ϊ��A��
��1��ͼ�У���OCE���ڡ�_____��
��2���������ߵĽ���ʽ��
��3�����������Ƿ���ڵ�P��ʹS��PAE=![]() S��CDE�������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
S��CDE�������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ǣ��ҵ�A��![]() ��a����B��sin����cos����b���� C����m2��2m��2��c�����ڶ��κ���y����x2��x��3��ͼ���ϣ���ôa��b��c�Ĵ�С��ϵ�� �� ����
��a����B��sin����cos����b���� C����m2��2m��2��c�����ڶ��κ���y����x2��x��3��ͼ���ϣ���ôa��b��c�Ĵ�С��ϵ�� �� ����
A. a��b��c B. a��c��b C. b��c��a D. c��b��a
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
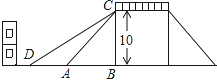
����Ŀ����ͼ��һ���������ŵ�ʾ��ͼ�����ŵĸ߶���10�ף�CB��DB������AC����б��Ϊ45����Ϊ�˷��������Ƴ������ţ��������ž��������¶ȣ�ʹ������DC���¶�Ϊi=![]() ��3�������½�������3�������е�������ԭ�½ǣ�A�㴦��10�Ľ������Ƿ���Ҫ��������ο����ݣ�
��3�������½�������3�������е�������ԭ�½ǣ�A�㴦��10�Ľ������Ƿ���Ҫ��������ο����ݣ� ![]() ��1.414��
��1.414�� ![]() ��1.732��
��1.732��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���P������Ϊ��0��2����ֱ��y=![]() ��x�ᡢy��ֱ��ڵ�A��B����M��ֱ��AB�ϵ�һ�����㣬��PM������СֵΪ�� ��
��x�ᡢy��ֱ��ڵ�A��B����M��ֱ��AB�ϵ�һ�����㣬��PM������СֵΪ�� ��

A��3 B��4 C��5 D��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�Rt��ABC�������㶼�ڸ���ϣ���A��B��C������ֱ�ΪA��-1��3����B��-3��1����C��-1��1���������������⣺
��1��������ABC����y��ԳƵ���A1B1C1����д��B1��������
��2��������A1B1C1�Ƶ�C1˳ʱ����ת90����õ�����A2B2C2��
��3�������A1�߹���·������
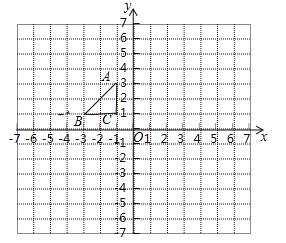
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com